The topics on this page are vector functions and space curves.
A function whose domain is a set of real numbers and whose range is a subset of 2-space (or called plane), or 3-space is called a vector-valued function of a real variable. For example, the line through a point P parallel to a nonzero vector U is the range of the vector-valued function r given by
![]()
Each t corresponds to a point, which can be thinked as a vector initiating from the origin and tip pointing at the point, in the straight line. See the graph below. Usually a vector-valued function in 2-space (resp. 3-space) has two component functions (resp. three component functions). Such as the staight line vector function in 2-space and 3-space can be written as
![]()
where point (a, b) (or (a, b, c)) is a point that the line passes through
and
(u1, u2) (or (u1, u2, u3)) is a vector parallel to the line.
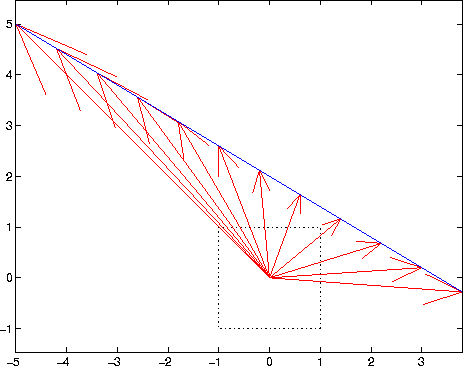 The graph above
is of the vector function of the straight line r(t) = ti
+
(-0.6t + 2)j = 2j + t(i - 0.6j). Second
expression shows that r passes through point (0, 2) and
is parallel
to vector (1,-0.6).
The graph above
is of the vector function of the straight line r(t) = ti
+
(-0.6t + 2)j = 2j + t(i - 0.6j). Second
expression shows that r passes through point (0, 2) and
is parallel
to vector (1,-0.6).
Let r(t) = f(t)i + g(t)j + h(t)k be a vector function in 3-space. As t runs through an interval I, the corresponding function values, which in this case are vectors, run through a set of points which we called the graph of the function r. If r is continuous on I, such a graph is called a space curve; more specifically, the curve described by r. Or we say the space curve is parametrized by r(t). The interval I is called a parametric interval; each t in I is called a parameter. An interesting example of space curve is the helix.
If the point (x, y, z) revolves around z-axis at a distance a from it and simultaneously moves parallel to z-axis in such a way that its z-component is proportional to the angle of revolution, the resulting path is called circular helix. If t denotes the angle of revolution, we have
![]()
where a is greater than zero, and b is nonzero. When t varies from 0 to
2
![]() , the x- and y-coordinates return to their original values while z
changes from 0 to
, the x- and y-coordinates return to their original values while z
changes from 0 to
![]() .
. 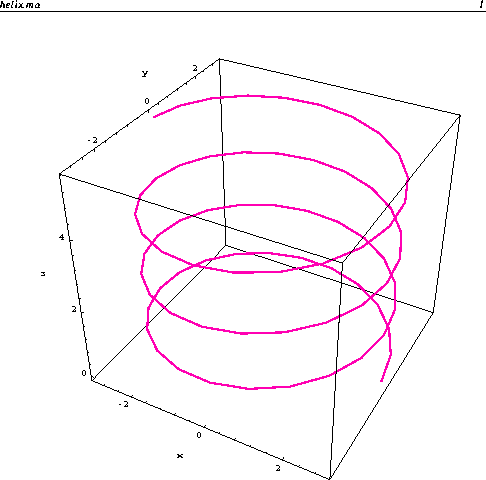 A graph is
shown above with a = 3 and b = 0.25 for
t from 0 to
A graph is
shown above with a = 3 and b = 0.25 for
t from 0 to
![]() .
.
The uaual operations of vectors can be applied to combined two vector functions or to combine a vector function with a real-valued function. If U and V are vector-valued functions, and if f is a real-valued function, all having a common domain, we define new functions U + V, fU, and U dot V by the equations
![]()
If U and V are in the space, we can also define the cross product by
![]()