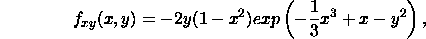The problem to find the minimum or maximum value of a function is encountered
very frequently in geometry, mechanics, physics, and other fields. It was
one
of the principal incentives for the development of the calculus in the
seventeenth century. Our object for this page is to give a means of locating
the extrema of two variable functions.
Recall the same problem in the case of single veriable function. We locate
all critical points by solving f'(x) = 0. It is the same as to find all
points with horizontal tangent line since at the points where a differentiable
function attains relative maximum or minimum the tangent line is
horizontal.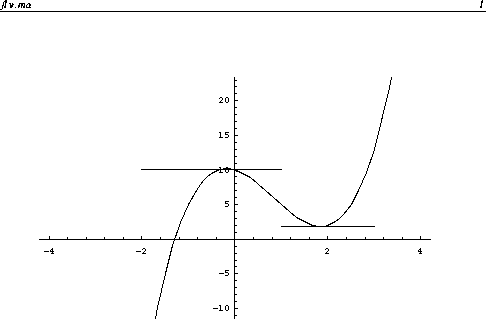 Similarly, for the case of a two variable differentiable
function f(x, y), we look for those points (also called critical or
stationary points) whose tangent planes are
horizontal.
Similarly, for the case of a two variable differentiable
function f(x, y), we look for those points (also called critical or
stationary points) whose tangent planes are
horizontal.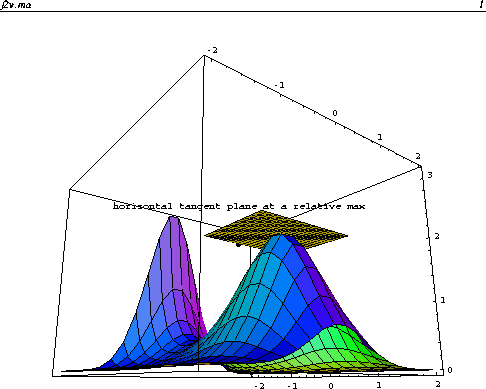 Since the normal vector of tangent plane at (a,
b) for the surface z = f(x,
y)
is
Since the normal vector of tangent plane at (a,
b) for the surface z = f(x,
y)
is
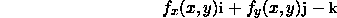
we want to solve
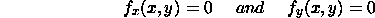 and
and
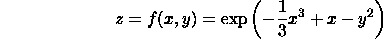 for critical points
because horizontal planes have normal vector parallel to z-axis, i.e. (0,
0, 1) or (0, 0, -1).
for critical points
because horizontal planes have normal vector parallel to z-axis, i.e. (0,
0, 1) or (0, 0, -1).
- Example 1
Find all critical points of the surface
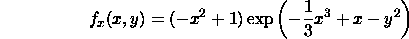 .
.
- Solution
First of all, we compute
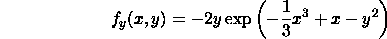
Set both partial derivatives zero, we have x = 1, or -1 and y = 0. Therefore
(1, 0) and (-1, 0) are the critical points of f.
In the single variable problem, we have the rules
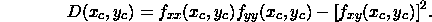
to categorize the nature of critical points. There is an analogous theory,
second-derivative test for extrema, for functions of two variables:
- Theorem Suppose (a, b) is a stationary point of a
function f(x, y) with continuous second order partial derivatives in a domain
containing (a, b). Let
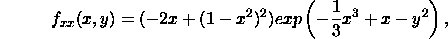
and let
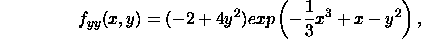
Then we have:
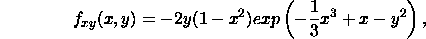
With this theorem we can summarize the procedure to find the extrema
of a twice
diffenentiable function f(x, y) of two variables as follows:
- Step 1
Locate the critical points by solving
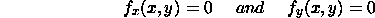 and
and
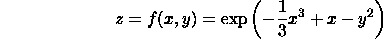 .
.
- Step 2
Compute second partial derivatives
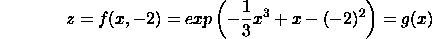 and
and
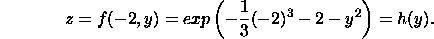 and evaluate
the
and evaluate
the
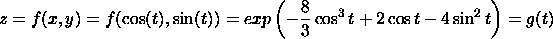 for each critical point found in step 1.
for each critical point found in step 1.
- Step 3
Use the Theorem above to categorize the nature of critical points. Then
compare their function values to find the absolute maximum or minimum.
- Step 4
If the function is restricted to a domain (finite) with boundary, we should
also search for the extrema along the boundary. It is then reduced to a
single
variable problem theoretically.
- Example 2
Find all relative maximums and minimums for the function
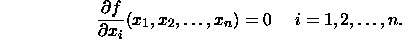
- Solution
- Step 1. Compute the first order partial derivatives and set
to zero.

we have x = 0 or 2 and y = 1 or -1. Thus (0, 1), (0, -1), (2, 1) and (2,
-1)
are the critical points of f.
- Step 2

After some computations, we have

Note that f is an exponential function, always positive.
- Step 3
From the Theorem, we know that f(0, 1) = exp(2/3) is a relative maximum and
f(2,-1) = exp(-14/3) is a relative minimum. At both (0, -1) and (2, 1),
f
has saddle points.
Along y = 0, x-axis, it is easy to see that

It shows that f can grow as big as possible when x tends to infinity and
as
close to zero as well when x tends negative infinity (note f is positive
for
all (x, y)), so we conclude that f has no absolute maximum nor absolute minimum
over xy-plane.
Suppose the problem was further restricted to the region R bounded by y =
-x +
4 and
 , then we have more (step 4) to search for the possible extrema
along boundaries. In this case, only (2, 1) and (2, -1) are inside R, they
are still saddle point and relative minimum respectively.
, then we have more (step 4) to search for the possible extrema
along boundaries. In this case, only (2, 1) and (2, -1) are inside R, they
are still saddle point and relative minimum respectively.
- Step 4
The restriction of f on the boundary of R can be expressed as

respectively. Both are reduced to single variable problems. Readers should
be
able to find the maximums and minimums on each restriction. To determine
the
absolute extrema on the region R, you need to compare the function values
of
all critical points obtained in step 3 and 4 and corner points, such as the
intersection points of two boundary curves.
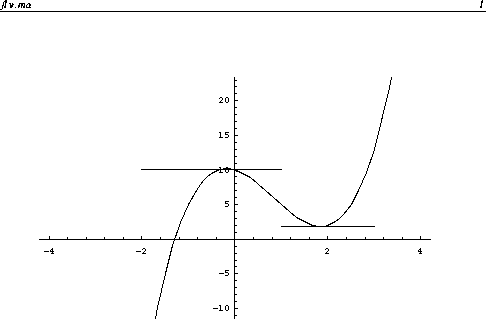 Similarly, for the case of a two variable differentiable
function f(x, y), we look for those points (also called critical or
stationary points) whose tangent planes are
horizontal.
Similarly, for the case of a two variable differentiable
function f(x, y), we look for those points (also called critical or
stationary points) whose tangent planes are
horizontal. Since the normal vector of tangent plane at (a,
b) for the surface z = f(x,
y)
is
Since the normal vector of tangent plane at (a,
b) for the surface z = f(x,
y)
is