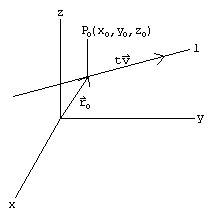
A line is determined by a point and a direction. Thus, to find an equation representing a line in three dimensions choose a point P_0 on the line and a non-zero vector v parallel to the line. Since any constant multiple of a vector still points in the same direction, it seems reasonable that a point on the line can be found be starting at the point P_0 on the line and following a constant multiple of the vector v (see the figure below).

If r_0 is the position vector of the point P_0, then the line must have the form
![]()
This is the vector equation of a line in three dimensions. By letting r=<x,y,z>, r_0=<x_0,y_0,z_0>, and v=<a,b,c> we obtain the equation
![]()
which leads to the parametric equations of the line passing through the point P_0=(x_0,y_0,z_0) and parallel to the vector v=<a,b,c>:
![]()
To find the parametric equations of the line passing through the point (-1,2,3) and parallel to the vector <3,0,-1>, we first find the vector equation of the line. Here, r_0=<-1,2,3> and v=<3,0,-1>. Thus, the line has vector equation r=<-1,2,3>+t<3,0,-1>. Hence, the parametric equations of the line are x=-1+3t, y=2, and z=3-t.
It is important to note that the equation of a line in three dimensions is not unique. Choosing a different point and a multiple of the vector will yield a different equation. If we had taken the point to be (2,2,-4) and the vector to be <-6,0,2> in the previous example we would have found the parametric equations of the line to be x=2-6t, y=2, and z=-4+2t. This is representation of the line is equivalent to the one found above.
There is a third representation of a line in three dimensions. Consider solving each of the parametric equations for t and then setting them equal:
![]()
These are the symmetric equations of the line. Note that we must have a, b, and c non-zero to use this representation; the line in the example above would have symmetric equations
![]()
Where does the line in the previous example intersect the xy-plane? Well, the line intersects the xy-plane when z=0. From the parametric equation for z, we see that we must have 0=-3-t which implies t=-3. Thus, x=-1+3t=-10 and y=2. The line intersect the xy-plane at the point (-10,2).
A plane is determined by a point P_0 in the plane and a vector n (called the normal vector) orthogonal to the plane. If P is any other point in the plane and r_0 and r are the position vectors of the points P_0 and P, respectively, then an equation of the plane is
![]()
since each vector in the plane must be orthogonal to the normal vector n and the vector r-r_0 is a vector in the plane. Either of these equations is called a vector equation of the plane. With the substitutions n=<a,b,c>, r=<x,y,z>, and r_0=<x_0,y_0,z_0> and some simplification we have an equation of the plane passing through the point P_0(x_0,y_0,z_0) with normal vector <a,b,c>:
![]()
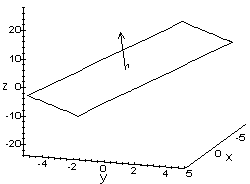
This is frequently written as ax+by+cz=d. Notice that the normal vector can be identified directly from the coefficients on the left hand side of the equation: n=<a,b,c>. As with equations of lines in three dimensions, it should be noted that there is not a unique equation for a given plane. The graph of the plane -2x-3y+z=2 is shown with its normal vector.
Find an equation of the plane passing through the points P(1,-1,3), Q(4,1,-2), and R(-1,-1,1). Since we are not given a normal vector, we must find one. By taking the cross product of the vector a from P to Q and the vector b from Q to R, we obtain a vector which is orthogonal to each of the original vectors (and thus orthogonal to the plane). Hence, a=<3,2,-5>, b=<-5,-2,3>, and

So, an equation of the plane is
![]()
-4(x-1)+16(y+1)+4(z-3)=0 which implies -4x+16y+4z=-8
Two planes are parallel if their normal vectors are parallel (constant multiples of one another). It is easy to recognize parallel planes written in the form ax+by+cz=d since a quick comparison of the normal vectors n=<a,b,c> can be made.
Find the formula for the distance D from a point P_0(x_0,y_0,z_0) to the plane ax+by+cz+d=0. Let P_1(x_1,y_1,z_1) be any other point in the plane. Let r =<x_0-x_1,y_0-y_1,z_0-z_1> be the vector from P_1 to P_0. Then, from the figure above, the distance D from the point to the plane is the scalar projection of the vector r onto the normal vector n:
![]()
But, since the point P_1 lies in the plane, -ax_1-by_1-cz_1=d. Hence, the distance D from the point P_0 to the plane is
![]()
[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.