
There are many situations when we might wish to know whether a set of vectors is linearly dependent, that is if one of the vectors is some combination of the others.
Two vectors u and v are linearly independent if the only numbers x and y satisfying xu+yv=0 are x=y=0. If we let

then xu+yv=0 is equivalent to
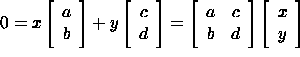
If u and v are linearly independent, then the only solution to this system of equations is the trivial solution, x=y=0. For homogeneous systems this happens precisely when the determinant is non-zero. We have now found a test for determining whether a given set of vectors is linearly independent: A set of n vectors of length n is linearly independent if the matrix with these vectors as columns has a non-zero determinant. The set is of course dependent if the determinant is zero.
The vectors <1,2> and <-5,3> are linearly independent since the matrix
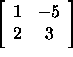
has a non-zero determinant.
The vectors u=<2,-1,1>, v=<3,-4,-2>, and w=<5,-10,-8> are dependent since the determinant
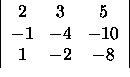
is zero. To find the relation between u, v, and w we look for constants x, y, and z such that
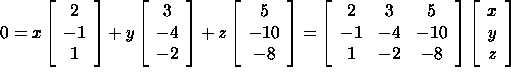
This is a homogeneous system of equations. Using Gaussian Elimination, we see that the matrix
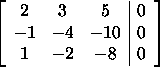
in row-reduced form is
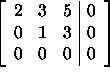
Thus, y=-3z and 2x=-3y-5z=-3(-3z)-5z=4z which implies 0=xu+yv+zw=2zu-3zv+zw or equivalently w=-2u+3v. A quick arithmetic check verifies that the vector w is indeed equal to -2u+3v.
[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.