Green's theorem relates the value of a line integral to that of a double integral.
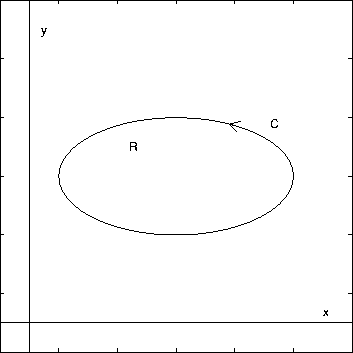
Let C be a positively oriented, piecewise smooth, simple closed curve that bounds the region R in the xy plane. Let us define the terms in this last sentence. Positively oriented means that C is traversed in a counter-clockwise manner. Simple means that C does not intersect itself between its endpoints. (For example, a curve in the shape of a figure 8 is not simple.) If we parameterize C by the vector function r(t) with a<=t<=b, then closed means r(a)=r(b). See the figure below:

Green's Theorem states that
![]()
Here it is assumed that P and Q have continuous partial derivatives on an open region containing R.
Example
Evaluate the line integral
![]()
where C is the boundary of the square R with vertices (0,0), (1,0), (1,1), (0,1) traversed in the counter-clockwise direction.
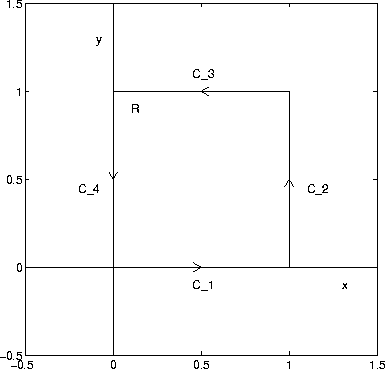
To do the above integration 4 line integrals, one for each side of the square, must be evaluated. (In this case C = C_1+C_2+C_3+C_4.) This is a good case for using Green's theorem. We have
![]()
Hence,
![]()
The region R in this case is square, so the double integral becomes the iterated integral
![]()
The iterated integral can be evaluated in a straightforward manner, yielding the result 2.
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.