The method of undetermined coefficients is a technique
for determining the
particular solution to linear
constant-coefficient differential equations
![]()
for certain types of nonhomogeneous terms f(t).
This section will cover:
Nonhomogeneous term f(t)=exp(at)
Consider the example:
![]()
We guess that the particular solution has the form
y_p(t)=Aexp(3t). Here
A is a unknown constant. In this
case we have y'_p=3Aexp(3t) and
y''_p=9Aexp(3t).
Substituting the expressions for y_p, y'_p, and y''_p
into the differential equation, we obtain
![]()
The LHS of this last expression is 20Ae^3t. Comparing
the two sides of
the differential equation, we conclude
that A=1/20.
The approach for this example is standard for a
constant-coefficient
differential equations with
exponential nonhomogeneous term. If the
nonhomogeneous
term is constant times exp(at), then the initial guess
should be Aexp(at), where A is an unknown coefficient
to be determined.
This guess may need to be
modified.
Nonhomogeneous term f(t)=polynomial
Consider the example:
![]()
We guess that the particular solution has the form
y_p(t)=At+B, where A
and B are unknowns. In this
case we have y_p=A and y_p=0. Substituting
the
expressions for y_p, y'_p, and y''_p into the
differential equation, we
obtain
![]()
Rearranging the LHS of this equation, we obtain
![]()
Comparing the coefficients of t on both sides of the
equation, we conclude that
2A=1. Comparing the
constant terms, we conclude that 3A+B=1. The first
equation implies A=1/2. This fact and the second
equation imply that B=-1/2.
If the nonhomogeneous term is a polynomial of degree n,
then an initial guess
for the particular solution should
be a polynomial of degree n:
![]()
This guess may need to be modified.
Nonhomogeneous term f(t)=sine or cosine
Consider the example:
![]()
We guess that the particular solution is
y_p=Asin(3t)+Bcos(3t). Note that
we have both sine
and cosine terms. In this case we have
![]()
Substituting y_p, y'_p, and y''_p into the differential equation we obtain:
![]()
Rearranging the LHS of this equation, we obtain:
![]()
Comparing the coefficents of sin(3t) on both sides of
the equation, we
conclude -7A-9B=1. The RHS has no
cosine terms. This means that the
coefficient of
cosine on the LHS must be 0 - that is, 9A-7B=0.
Solving
these equations we conclude
A=-7/130 and B=-9/130.
In general if the nonhomogeneous term is
of the form a*sin(ct)+b*cos(ct).
Then an
initial guess for the particular solution is
y_p=Asin(ct)+Bcos(ct).
This guess may need to be modified.
Consider the differential equation
![]()
If the nonhomogeneous term is a sum of two terms, then
the particular
solution is y_p=y_p1 + y_p2, where
y_p1 is a particular solution of
y''+3y'+2y=exp(3t)
and y_p2 is a particular solution y''+3y'+2y=sin(3t).
From our discussion
above, we know y_p1=exp(3t)/20 and that
y_p2=(t-1)/2. Hence the complete
particular solution is
y_p=exp(3t)/20+(t-1)/2. Remember the initial
guesses above
may need to be modified.
Consider the example:
![]()
According to the arguments above, the guess for
the particular solution
is y_p=Aexp(-t). We
have y'_p=-Aexp(-t) and y''_p=Aexp(-t).
Substituting
these expressions into the ode, we have
![]()
The LHS of this expression equals 0! Hence, we have
![]()
which is inconsistent. This means that the initial
guess y_p=Aexp(-t) is
not appropriate. The reason
is that exp(-t) is a solution to the homogeneous
equation y''+3y'+2y=0. (Note that the characteristic
equation is
r^2+3r+2=(r+2)(r+1)=0.)
The appropriate guess in this case is y_p=Atexp(-t).
We have
y_p=Aexp(-t)-Atexp(-t) and
y''_p=-2Aexp(-t)+Atexp(-t).
Substituting into the
ode we have,
![]()
Cleaning up the LHS, we have Aexp(-t)=exp(-t). Hence, A=1.
The moral of this story is we must multiply an initial
guess for the
particular solution by t^s, where s
is the smallest integer so that no
term in the modified
particular solution is a solution to the homogeneous
ode. Here are a couple
of examples:
![]()
Two linearly independent solutions to the ode are
listed. As an initial
guess, y_p=Aexp(-t). The modified
guess is y_p=At^2exp(-t). We
need to multiply by t^2
since texp(-t) is a solution to the homogeneous ode.
Another example:
![]()
As an initial guess, y_p=At+B. The term B, a constant
is a solution to the
homogeneous part. Hence, the
modified guess is y_p=At^2+Bt.
The following table gives the form of the particular
solution for various
nonhomogeneous terms.
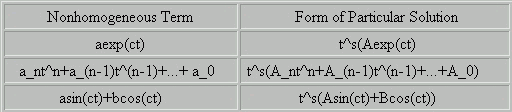
Recall that s is the smallest integer such that no term in the particular
solution is
is a solution to the homogeneous differential
equation.
[ODE Home] [1st-Order Home] [2nd-Order Home] [Laplace Transform Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.