The general form of a homogeneous Euler-Cauchy ODE is
![]()
where p and q are constants. The coefficients of y' and y
are discontinuous
at t=0. This means that the solution to
the differential equation may not be
defined for t=0.
The existence and uniqueness theory states that a solution
exists on any interval (a,b) not containing t=0.
Recall that the general solution of the ode is
![]()
where C1 and C2 are constants and y1(t) and y2(t) are
two linearly
independent solutions of the ode.
Solution Procedure
We first multiply the differential equation by t^2 to get
![]()
We now make the guess:
![]()
where r is a constant to be determined. (For simplicity, we will assume that t>0 in this calculation. It can be shown that the most general solution is |t|^r. We give the general solution with absolute value signs below.) With this guess we have
![]()
Substituting these expressions into the ode, we have
![]()
This equation is satisfied if t^r=0 or
r(r-1)+pr+q=0. The condition t^r=0 is
satisfied if
t=0 or t=infinity. These are considered as degenerate
cases and
are neglected. Hence, r must satisfy
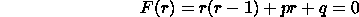
F(r) is called the characteristic polynomial. Solving the
original ode is
reduced to solving an algebraic equation.
Assuming the coefficients p and q are real numbers, there
are three
cases to consider:
Characteristic Polynomial has Distinct Roots
Suppose that the characteristic polynomial has two distinct,
real roots
(call them a and b). Then |t|^a and |t|^b are
linearly independent solutions
to the original ode and
the general solution to the ode is:
![]()
Consider the following example:
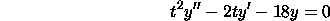
The characteristic polynomial is r(r-1) - 2r -18 = (r - 6)(r +3),
which
has roots 6 and -3.
![]()
Characteristic Polynomial has a Double Root
Suppose that the characteristic polynomial has a double root
(call it a).
y_1(t)=|t|^a is one solution to differential equation.
We need a second
linearly independent solution to the ode to
get the general solution. Using
the technique of
reduction of order, it can be shown
that t^a log(|t|) is also
a solution
of the ode. The general solution is
![]()
Consider the following example:
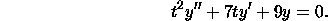
The characteristic polynomial is r(r-1) + 7r + 9 = (r + 3)^2,
which has a
double root -3. The general solution is
![]()
Complex-Conjugate Roots
Suppose that the characteristic polynomial has complex
roots a+ib and a-ib,
where a and b are real. These are distinct
roots, so the the general solution
can be written:
![]()
The problem with writing the solution in this form is
that it involves
complex-valued functions. It is possible
to re-express the general solution
in terms of two linearly
independent real-valued functions.
Note that
![]()
Here we have used Euler's identity. Hence,
![]()
Similarly, we have
![]()
Substituting, these two expressions into the general solution we have
![]()
Choose C_1=0.5 and C_2=0.5. This yields the solution:
![]()
Now choose C_1=-i0.5 and C_2=i0.5. This yields the solution:
![]()
Both of these functions are solutions to the original ode. In
addition, they are
linearly independent, since they are not
multiples of each. Hence, any solution
to the ode can be
expressed in terms of these functions. So we can write:
![]()
for real numbers D_1 and D_2 are constants.
Consider the example:

The characteristic polynomial is r(r-1) - 6r + 13.
Using the
quadratic formula,
we find that the roots are 3 + 2i and 3 - 2i.
Hence, the general solution can be
written:
![]()
[ODE Home] [1st-Order Home] [2nd-Order Home] [Laplace Transform Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.