The Laplace Transform method is a technique for solving
linear differential
equations with initial conditions.
It is commonly used to solve electrical
circuit
and systems problems.
What is a Transform Method?
The simplest way to describe a transform method is to
consider an example.
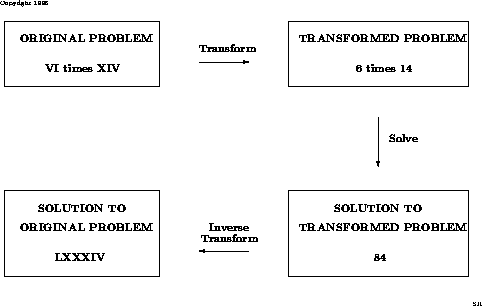
Suppose we wish to compute the
product of VI and XIV, both Roman numerals,
and express
the answer as a Roman numeral. Unless you are a Roman(!),
the
first thing to do is transform the Roman numerals to Arabic
numerals. VI is 6
and XIV is 14. The transformed problem is:
compute the product
of 6 and 14. We
can all do this! The solution to the transformed problem
is 84. We then convert
the solution of the transformed problem
to the solution to original problem. 84 in
Roman numerals is
LXXXIV. This last step is called the inverse transformation.
The following
diagram summarizes what we have done.

Why use a transform method? Some problems are difficult to solve
directly.
With a transform method, the hope is that the transformed problem
is easy
to solve. That is certainly the case for the simple example above.
One must
also take into account the difficulty of transforming the original
problem
and inverse transforming the solution to the transformed problem.
Consider the following differential equation: y'+y=0 with initial
condition
y(0)=3. This is a linear
first-order differential equation and the exact solution
is
y(t)=3exp(-t). One doesn't need a transform method to solve this problem!!
Suppose we solve the ode using the Laplace Transform Method. Instead
of
solving directly for y(t). We solve for its partner function. Let's
call it Y(s).
Y(s) is the solution of the equation sY(s)-3+Y(s)=0. We
will learn how to
determine the transformed
equation later. The key point
is that the transformed
problem is a LINEAR ALGEBRAIC PROBLEM. We have
converted a linear
differential equation into a linear algebraic problem.
It is much easier to solve
a linear algebraic problem than a linear
differential equation. The solution to the
transformed problem is
Y(s)=3/(s+1). We must now transform Y(s) to a
function of t.
It will
be shown that the function of t associated with 3/(s+1) is
precisely
3exp(-t).
[ODE Home] [1st-Order Home] [2nd-Order Home] [Laplace Transform Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.