Qualitative Analysis of Non-Autonomous First-Order ODE

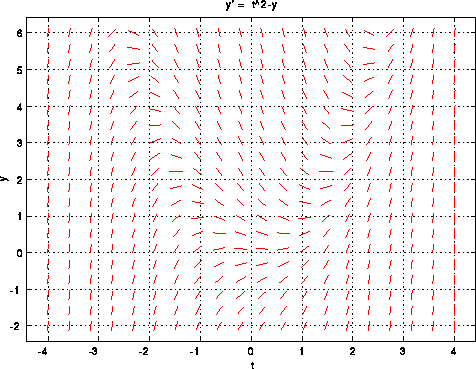
Consider the non-autonomous ode y'=t^2-y. The differential equation
gives a formula for the slope. The slope depends on both the dependent and
independent variables.

Direction Fields

A direction field consists of small lines which are tangent to a solution y(t)
of the ode at each point in the t-y plane. For the differential equation
y'=t^2-y, the function f(t,y)=t^2-y gives the slope of a solution y(t). For t=2
and y=1 the slope is 3. This means that if y(t) passes through (2,1), then
y'(t)=3. The following plot shows the direction field for the model differential
equation.

Notice that at t=2 and y=1, the small line has positive slope. It is
approximately 3, indicating that a solution passing through this point has
slope 3.

Sketching Solutions

The direction field gives a rough idea about solutions to the differential
equation, since solutions to the differential equation are tangent to the small
slope lines. The following plot draws in the solutions.

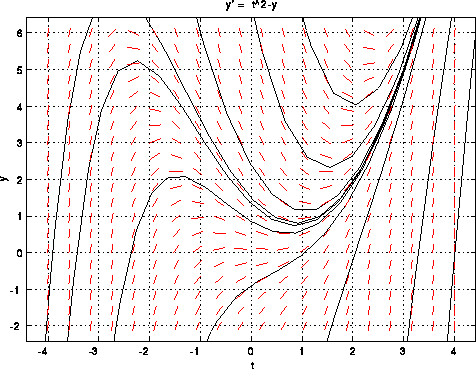
This plot gives a rough idea of behavior of solutions to the ode without
having to solve ode. Note that there are several solution curves. Why? Each
solution corresponds to a differential initial condition. If an initial condition is
specified, like y(0)=1, then the curve throught t=0 and y=1 is the solution to
the differential equation and the initial condition.

Isoclines

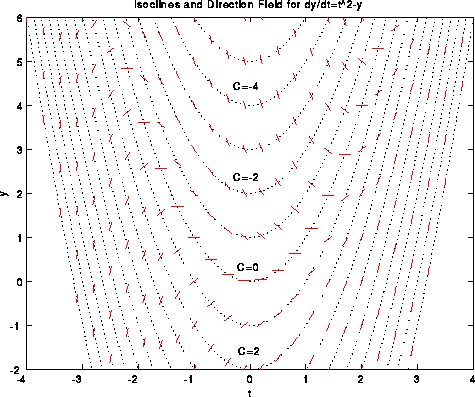
The procedure for drawing the direction field can be simplified by first sketching
isoclines. An isocline is a curve in the t-y plane on which the derivative of
solutions to the differential equation is constant. For example, where is the
derivative of solutions to the model ode equal to 3? We have y'=t^2-y=3. Henc
on the curve t^2-y=3 or y=t^2-3, the derivative is 3. On the curve t^2-y=C, the
derivative of solutions to the ode is C. The following plot shows isoclines for various
values of C and the derivative of solutions to the model ode on each isocline.

Summary

Here is a summary of the procedure for doing a qualitative analysis of
non-autonomous ode y=f(t,y)

1. Sketch isoclines. These are curves of the form f(t,y)=C, where C is
   a constant, for several values of C. Alternatively, one can draw in the
   direction field by drawing tangent lines at a whole bunch of points in the
   t-y plane, without using isoclines, as in the first plot above.
2. Draw direction field. On the isocline corresponding to constant C, the
   derivative of the solution to the ode has slope C. Draw tanget lines with
   slope C.
3. Sketch in solutions. Remember, solutions do not intersect.

[ODE Home] [1st-Order Home] [2nd-Order Home] [Laplace Transform Home] [Notation] [References]

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.