Qualitative Analysis of Autonomous ODE

Consider the autonomous ode y'=4y(1-y). The differential equation gives
a formula for the slope. In this example, the slope just depends on the
independent variable. If the function passes through the point (1,2), the slope
is -8. The slope is independent of t, so the slope is constant if y is constant.
The following table lists the slope at several y points.

Slopes for Model ODE

Direction Fields

The direction field consists of small lines which characterize the slope of y(t)
at each point in the t-y plane Here is the direction field for our example.

For example, if y(t) passes through the point (1,2) it should have a slope of -8.
This is shown by the small line with large negative slope. If y(t) passes through
(1,0.5), the slope is 1, and this shown by the line with moderate positive slope.

Sketching Solutions

The direction field gives us a rough idea about solutions to the differential
equation, since solutions to the differential equation are tangent to the small
slope lines. The following plot draws in the solutions.

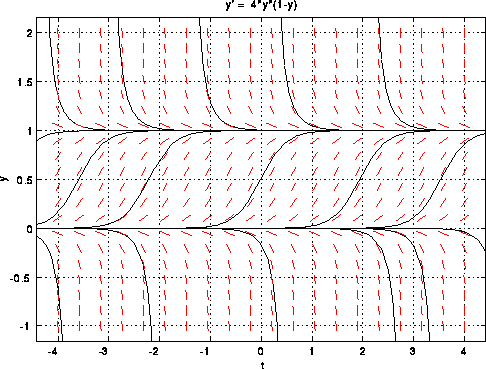
The plot above gives us qualitative information about solutions to the
differential equation. There are several points to note:

• Note that there are several solution curves. Actually, the ode has an
  infinite number of solutions. Why? Each solution corresponds to a different
  initial condition. For example, if y(0)=0.5, then we have a solution that
  apparently increases to 1 as t -> infinity.

• y(t)=0 and y(t)=1 are solutions to the differential equation. This is easy to
  verify. If y=1, for example, then y'=0 and 4y(1-y)=0. Hence, the differential
  equation is satisfied. A similar calculation shows that y=0 is a solution to the
  ode. In general, for an autonomous ode of the form y'=f(y), the zeros of f(y)
  are constant solutions to the ode. We verify this: let y(t)=c. Then y'=0 and
  f(y)=f(c)=0, and the ode is satisfied.

• We can extract a lot of information about solutions to the ode from the
  plot above without knowing the precise mathematical formula for the
  solution.
  

  • If initially y>1, then y->1 as t-> infinity
  • If initially y=1, then y=1 for all t
  • If initially 0<y<1, then y->1 as t-> infinity
  • If initially y=0, then y=0 for all t
  • If initially y<0, then y-> negative infinity as t-> infinity
    

  The above conclusions are based on the fact that two solutions to an ode
  do not, in general, intersect. Although is looks as if solutions intersect with
  the lines y=0 and y=1, they are in fact asymptotic to these lines.
  
  

Summary

Here is a summary of the procedure for doing a qualitative analysis of
autonomous ode y'=f(y).

1. Determine the constant solutions to the differential equation. These
   are of the form y=c, where c is a root of f(y). There may be no constant
   solutions, a finite number of constant solutions, or an infinite number
   of constant solutions.
2. Make a table of slope as a function of y, as above.
3. Using the info in the table, draw a direction field.
4. Sketch in solutions. The constant solutions should be put in first. Use
   the direction field to sketch other solutions. Remember, solutions do not
   intersect.

[ODE Home] [1st-Order Home] [2nd-Order Home] [Laplace Transform Home] [Notation] [References]

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.