This page reviews the following aspect of differentiation:
The Definition of the Derivative
Although you will likely not use the definition to compute derivatives in later calculus courses, you should nevertheless know the definition of the derivative. The derivative of f with respect to x is given by
![]()
when this limit exists.
If f(x) and g(x) are differentiable functions, then the derivative of the product fg with respect to x is given by
(fg)' = f 'g + f g'
This can be fairly easily derived from the definition.
Example
To calculate the derivative of h(x) = x2ex we must use the product rule:
![]()
If f(x) and g(x) are differentiable functions and g(x) is not equal to zero, then the derivative of the quotient f/g is
![]()
which can be remembered with the saying "bottom-derivative-top minus top-derivative-bottom over bottom squared". Although a little harder to do, this result can be derived from the definition. Alternatively, the chain rule can be used to more easily establish this result.
Example
We can use the quotient rule to differentiate
![]()
Proceeding we have
![]()
If f(x) and g(x) are differentiable functions, then the derivative of the composition of g with f is
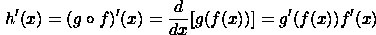
where the notation g'(f(x)) means the function g'(x) evaluated at f(x). Once again, this result can be established from the definition.
Example
Since the function h(x) = (2x4 + 3x)8 = g(f(x)) is really the composition of the function g(x) = x8 with f(x) = 2x4 + 3x, the derivative of h is
h'(x) = (g o f)'(x) = g'(f(x))f '(x) = 8(2x4 + 3x)7(8x3 + 3)
Example
Differentiate
![]()
We must use all three of the rules we have established (and in the proper order no doubt). The trick is to work from the outside in. The general structure of the function a fraction; thus, we must use the quotient rule:
![]()
But, we notice that in order to carry out the differentiation of the top and bottom terms in the numerator we must use the chain and product rules, respectively. Therefore,
![]()
which upon simplification becomes
![]()
Examples Involving Partial Derivatives
Often when carrying out partial differentiation we must use the product, quotient, and chain rules. Several examples follow.
Example
Differentiate f(x,t) = cos(x t2) with respect to t. We must use the chain rule with x held constant. Thus,
![]()
Example
Differentiate the following function with respect to y:
![]()
To do this, we of course view x as a constant. We see that the product rule must be used since we have a product of two functions involving y.
![]()
But, in taking the derivative of each of the functions sin(x + y) and e^(y2), we must use the chain rule:
![]()
![]()
Thus,
![]()
Example
To differentiate
![]()
with respect to x, it appears we must use the quotient rule. This is actually not the case. Since t is held constant, the denominator is a constant; the only x term appears in the numerator. Thus, the derivative is
![]()
[Sequences and Series Home] [Vector Calculus Home] [Math 254 Home] [Math 255 Home] [ODE Home] [Notation]
Written by Kevin
Thompson
Copyright ©
1996 Department
of
Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.