![]()
is called a p-series. In general, a p-series follows the following form:
![]()
p-series are useful because of the following theorem:
The p-series
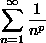
is convergent if p > 1 and divergent otherwise.
Unfortunately, there is no simple theorem to give us the sum of a p-series. For instance, the sum of the example series is
![]() .
.
If p=1, we call the resulting series the harmonic series:
![]()
By the above theorem, the harmonic series does not converge.
If you have questions or comments, don't hestitate to contact us.