Generally, it is possible to approximate a reasonably smooth function quite well, by keeping enough terms in the Fourier series. However, in the case of a function that has a finite number of discontinuities, the approximation of the function will always “overshoot” the discontinuity. This overshoot phenomenon gets sharper and sharper, i.e. bigger amplitude over a smaller domain, as the number of terms in the approximation is increased.
An example of the Gibbs phenomenon is shown in Figure 1.
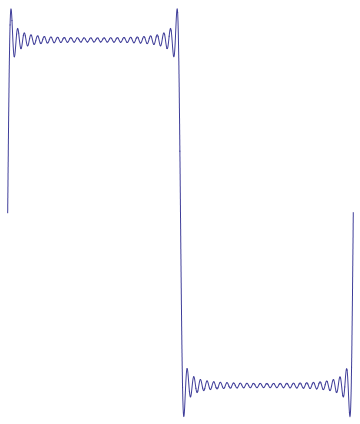
Figure 1: The Gibbs phenomenon for the Fourier series of a step function.