Two identical lumps of clay of (rest) mass $m$ collide head on, with each moving at $\frac35 c$. What is the mass of the resulting lump of clay?
First solution: We assume this is an elastic collision, that is, we do not worry about the details of the actual collision. Conservation of momentum doesn't help here — there is no momentum either before or afterwards. So we need to use conservation of energy. After the collision, there is no kinetic energy, so we have \begin{equation} E' = Mc^2 \end{equation} Before the collision, we know that the energy of each lump is \begin{equation} E = mc^2\cosh\alpha \end{equation} but how do we find $\alpha$? We are given that each lump is moving at ${3\over5}c$. But this means we know \begin{equation} \tanh\alpha = {3\over5} \end{equation} Yes, we could now use the formula $\cosh\alpha={1\over\sqrt{1-\tanh^2\alpha}}$, but it is easier to use a triangle. Since $\tanh\alpha={3\over5}$, we can scale things so that the legs have “lengths” 3 and 5. Using the (hyperbolic!) Pythagorean Theorem, the hypotenuse has “length” $\sqrt{5^2-3^2}=4$. This is just the triangle in Figure 4.3! Thus, \begin{equation} \cosh\alpha = {5\over4} \end{equation} and so \begin{equation} Mc^2 = E' = 2E = 2mc^2\cosh\alpha = {5\over2}\,mc^2 \end{equation} so that finally \begin{equation} M = {5\over2}\,m \end{equation}
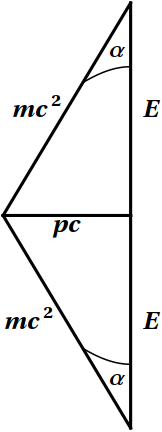 Figure 10.1: The momentum diagram for two colliding lumps of clay.
Figure 10.1: The momentum diagram for two colliding lumps of clay.
Second solution: Use conservation of 2-momentum, a vector quantity. That is, draw a momentum diagram, similar to a spacetime diagram but with units of either momentum (or, more commonly, energy), showing the 2-momenta both before and after the collision. Figure 10.1 shows such a diagram for the two lumps of clay. The initial configuration is represented by the two diagonal lines, one for each lump, moving in opposite directions; the final configuration is represented by the vertical line. Simple triangle trigonometry leads to the same computation as above, which can also be regarded as vector addition.