Angles are not Invariant
Regarding the antenna problem (§7.3), reader K. Vincent Jenner asks how the angles can be different for the spaceship's antenna and for a lightray traveling along it. He imagined putting the lightray inside a hollow antenna, which would seem to constrain the angles to be the same.
The same question could be raised in the Newtonian version of the problem, in which a ball is thrown along a mast. The computed angles are different, yet the ball clearly travels in the same direction as the mast (at least initially).
To resolve this apparent paradox, we must realize that there's a difference between position and velocity.
As shown in Figure 1, a ball thrown along a mast angled toward the rear will be seen from the dock to move in the direction the boat is moving (assuming the boat is moving fast enough…); the angle of the mast (backward) and of the ball's motion (forward) are clearly different, even though both observers see the ball move along the mast (until gravity visibly bends the trajectory).
So the angles are different, even though both observers agree that the ring moves along the mast — or that the lightray travels along the antenna!
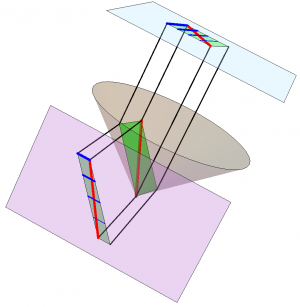
It is instructive to consider the three-dimensional spacetime diagram for the spaceship and the lightray shown in Figure 2. The ends of the antenna trace out the green worldsheet shown, and the lightray is shown in red moving along the light cone. Projecting vertically into two purely spatial dimensions, as shown above the lightcone, yields a “movie” showing the motion of both the antenna and the lightray, and reproduces Figure 1. Projecting horizontally into two spacetime dimensions, as shown in front of the lightcone, allows one to compare the speed of the spaceship with that of the lightray in the same direction (which is not the speed of light!), and is essentially a combination of Figures 7.8(b) and 7.9(b) in the text.
