- §1. The Surveyors
- §2. Spacetime Diagrams
- §3. Lorentz Transformations
- §4. Space and Time
- §5. Dot Product
Spacetime Diagrams
What is a spacetime diagram? Simply a diagram showing both where things are, and when they were there. For example, the first diagram in Figure 5.1 represents somebody sitting still (but getting older!), and the second diagram in Figure 5.1 represents somebody moving to the right at constant speed. Such trajectories are called worldlines. One early French railroad timetable shows the worldlines of each train! In relativity, the convention is to have the $t$-axis be vertical, and the $x$-axis be horizontal.
The Surveyors' Parable tells us that we should measure space and time in the same units, not meters and seconds, but both in either meters or seconds. We choose meters; this amounts to using $ct$ to measure time rather than $t$. In either case, light beams play a special role in spacetime diagrams, because they are drawn at $45^\circ$.
One fundamental geometric difference between circle trigonometry and hyperbola trigonometry is the presence of asymptotes in the hyperbolic case. These asymptotes have physical significance! Recall that (inverse) slopes in a spacetime diagram correspond to speeds; the asymptotes correspond to the existence of a “special” speed, namely the speed of light.

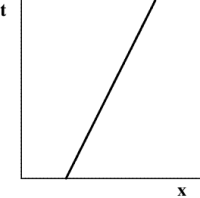
Figure 5.1: Spacetime diagrams representing standing still and moving to the right at
constant speed.