A useful technique in exploring an unknown geometry is to follow light beams, which leads to the use of null coordinates. Equivalently, factor the line element.

In Minkowski space, we have \begin{equation} ds^2 = dx^2 - dt^2 = (dx+dt)(dx-dt) \end{equation} Thus, introduce coordinates \begin{align} u &= t-x \\ v &= t+x \end{align} which brings the line element to the form \begin{equation} ds^2 = -du\,dv \end{equation} Why are null coordinates useful? Because the surfaces (curves) along which $u$ or $v$ is constant are lightlike.

Apply this idea to the Rindler geometry. Along a lightlike curve, we have \begin{equation} 0 = ds^2 = -\rho^2\,d\alpha^2 + d\rho^2 \end{equation} so that \begin{equation} d\alpha \pm \frac{d\rho}{\rho} = 0 \end{equation}

Figure 1: The null coordinates $(u,v)$, covering (only) the Rindler wedge.

We therefore introduce null coordinates via \begin{align} du &= d\alpha - \frac{d\rho}{\rho} \\ dv &= d\alpha + \frac{d\rho}{\rho} \end{align} Since we have been careful to separate variables, we can integrate these expressions to obtain \begin{align} u &= \alpha - \ln\rho \\ v &= \alpha + \ln\rho \end{align}

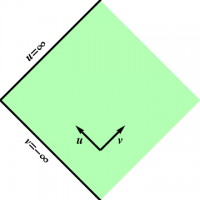
We must now regard $\rho$ as a function of $u$ and $v$ given by \begin{equation} 2\ln\rho = v-u \end{equation} or equivalently \begin{equation} \rho^2 = e^{v-u} \end{equation} Rewriting the line element in terms of our new coordinates ($u$,$v$) therefore yields \begin{equation} ds^2 = -\rho^2\,du\,dv = - e^{v-u}\,du\,dv \label{rmetuv} \end{equation} The $(u,v)$ coordinate system is shown in Figure 1. By using null coordinates, we have succeeded in “straightening out” the coordinate system, but it still only covers the Rindler wedge, with both $u$ and $v$ running from $-\infty$ to $+\infty$.

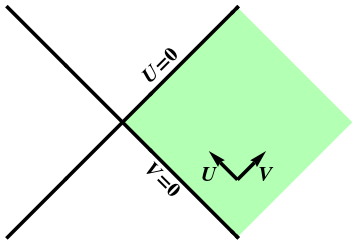Figure 2: The null coordinates $(U,V)$, covering all of Minkowski space.

However, the expression (\ref{rmetuv}) for the line element clearly factors, that is, \begin{equation} ds^2 = - \left(e^{-u}\,du\right) \left(e^v\,dv\right) = - d\left(-e^{-u}\right) d\left(e^v\right) \end{equation} We are therefore led to introduce yet another set of new coordinates \begin{align} U &= -e^{-u} = -\rho\,e^{-\alpha} \\ V &= e^v = \rho\,e^\alpha \end{align} and the rest is easy, since \begin{align} t &= \frac{V+U}{2} = \rho\sinh\alpha \\ x &= \frac{V-U}{2} = \rho\cosh\alpha \\ \end{align} The null coordinates $(U,V)$ are shown in Figure 2, and do, indeed, cover all of Minkowski space.

We have thus recovered Minkowski coordinates, defined on all of Minkowski space, starting from Rindler coordinates, defined only on a “Rindler wedge”. In the process, we have extended Rindler geometry across the “horizon” at $\rho=0$, which turns out to be nothing more than a coordinate singularity.

As we will see in § Black Holes for further details. the same process can be applied to the Schwarzschild geometry, and leads to a similar conclusion.