Recall from previous sections that the null geodesics of the Schwarzschild geometry satisfy \begin{align} \dot\phi &= \frac{\ell}{r^2} \\ \dot{t} &= \frac{e}{\left(1-\frac{2m}{r}\right)} \\ \dot{r}^2 &= e^2 - \left( 1-\frac{2m}{r} \right) \frac{\ell^2}{r^2} \label{ngeo} \end{align} Setting \begin{equation} u = \frac{1}{r} \end{equation} we have \begin{equation} \dot{r} = -\frac{1}{u^2} \dot{u} = -r^2 \dot{u} = -\ell \> \frac{\dot{u}}{\dot\phi} = -\ell \> \frac{du}{d\phi} \end{equation} so that the last equation in ($\ref{ngeo}$) becomes \begin{align} \left( \frac{du}{d\phi} \right)^2 &= \frac{e^2}{\ell^2} - ( 1-{2m}{u} ) \> u^2 \nonumber\\ &= \frac{e^2}{\ell^2} - u^2 + 2mu^3 \label{ngeo2} \end{align} Differentiating ($\ref{ngeo2}$) with respect to $\phi$ results in \begin{equation} \frac{d^2 u}{d\phi^2} = -u + 3mu^2 \label{ngeo3} \end{equation} which we rewrite in the form \begin{equation} \frac{d^2 (m u)}{d\phi^2} + m u = 3\,(m u)^2 \label{ngeo4} \end{equation} The right-hand side of ($\ref{ngeo4}$) is a relativistic correction to the corresponding Newtonian equation.

Assuming $mu\ll1$, we seek approximate solutions of ($\ref{ngeo3}$) of the form \begin{equation} u = u_0 + u_1 \epsilon \label{uapproxn} \end{equation} where $\epsilon$ is of order $mu$. Substituting ($\ref{uapproxn}$) into ($\ref{ngeo4}$) and collecting terms of the same order yields \begin{align} \frac{d^2 (m u_0)}{d\phi^2} + m u_0 &= 0 \\ \frac{d^2 (m u_1)}{d\phi^2}\>\epsilon + m u_1 \epsilon &= 3 (mu_0)^2 \end{align} The solution of the first equation is the straight line \begin{equation} u = \frac{1}{R} \sin\phi \label{nbend} \end{equation} where $R$ denotes the distance of closest approach to the origin, so that we could have taken \begin{equation} \epsilon = \frac{m}{R} \end{equation} A particular solution of the second equation is then \begin{equation} u_1 \epsilon = \frac{m}{R^2}(1+\cos^2\phi) \end{equation} so that our approximate solution for $u$ takes the form \begin{equation} u = \frac{1}{R} \sin\phi + \frac{m}{R^2}(1+\cos^2\phi) \label{bendeq} \end{equation}

 
Figure 1: The bending of null geodesics. The horizontal line represents the Newtonian solution (\ref{nbend}), which is a straight line, and the heavy line shows the approximate relativistic solution (\ref{bendeq}).

So our null geodesic is almost straight (the first term), and should in any case be nearly straight for $r$ large, that is for $u$ small. Noting that (\ref{bendeq}) implies that $\sin\phi<0$, the (small, positive) asymptotic values $\phi_1=2\pi-\phi$ (on the right) and $\phi_2=\phi-\pi$ (on the left) as $r$ approaches $\infty$ give the (asymptotic) orientation of the line, as shown in Figure 1. Since $u$ approaches zero as $r$ approaches $\infty$, we must have \begin{equation} -\frac{\phi_i}{R} + 2 \frac{m}{R^2} = 0 \end{equation} and the deflection angle is just the sum \begin{equation} \delta = \phi_1 + \phi_2 = 4 \frac{m}{R} = 4\frac{GM}{c^2 R} \end{equation}

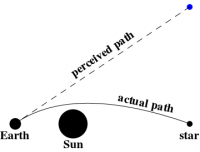
Since the mass of the sun is \begin{equation} m = 1.9891 \times 10^{33} \hbox{g} \end{equation} and its radius is \begin{equation} R = 6.955 \times 10^{5} \hbox{km} \end{equation} a light ray that just grazes the surface of the sun would be deflected by 1.75 seconds of arc, as shown schematically in Figure 2. Since this deflection is difficult to measure when the sun is shining, the best time to test this prediction of general relativity is during a total eclipse of the sun. The first expedition to attempt this was led by Sir Arthur Eddington in 1919; his observations confirmed Einstein's prediction, and helped make Einstein famous.