Consider now an (oriented) compact surface $\Sigma\in\RR^3$. Any such surface has a rectangular decomposition, that is, it can be covered by finitely many quadrilaterals, the sides of which are smooth curves, with the further assumption that any two such quadrilaterals overlap, if at all, either in a single common vertex or in a single common edge.

An example is given in Figure 1, which shows a single quadrilateral on the sphere, whose sides are not all geodesics. Arranging four such quadrilaterals next to each other around the sphere results in a quadrilateral cover of the sphere, although in this particular example the extra quadrilateral “caps” at the top and bottom would be circles.

Just as with the triangles in the previous section, we can consider the total curvature around one of these quadrilaterals. Since we are not assuming that the curves are geodesics, we have \begin{equation} \int K\,\omega + \oint \kappa_g\,ds = 2\pi - \sum (\pi - \eta_i) = \sum\eta_i - 2\pi \label{gb3} \end{equation}

since the sum now runs from $i=1$ to $i=4$. If we add up these expressions over the entire surface, that is, over all of our quadrilaterals, several things happen. First of all, $\kappa_g\,ds$ is being integrated twice over each edge, with opposite orientations. These integrals cancel, and the $\kappa_g$ term does not contribute overall. Furthermore, the sum over the interior angles $\eta_i$ is now a sum over all interior angles, which must add up to $2\pi$ at each vertex. This term thus becomes $2\pi v$, where $v$ is the number of vertices. Finally, there is a factor of $2\pi$ for each quadrilateral, that is, for each “face”, which contributes $2\pi f$, where $f$ is the number of faces. We have therefore shown that \begin{equation} \int_\Sigma K\,\omega = 2\pi v - 2\pi f \label{gb4} \end{equation} There is one further simplification. Since we assumed that each face is a quadrilateral, each face has four edges. However, each edge belongs to two faces, so that \begin{equation} e = \frac{4\,f}{2} \end{equation} where $e$ is the number of edges, which in turn implies that \begin{equation} e-f = f \end{equation} Putting this all together, we obtain the Gauss-Bonnet Theorem, which says that \begin{equation} \int_\Sigma K\,\omega = 2\pi (v - e + f) = 2\pi \chi(\Sigma) \label{gb5} \end{equation} where the last equality defines the Euler characteristic $\chi(\Sigma)$ of $\Sigma$.

Although we have only established the Gauss-Bonnet Theorem for decompositions in terms of quadrilaterals, it is a remarkable fact that the Euler characteristic does not depend on whether quadrilaterals are used, or arbitrary polygons. In other words, the Euler characteristic is a topological invariant of the surface, and we can compute it with any polygons we choose, including quadrilaterals.

The Gauss-Bonnet Theorem is even more remarkable than the Theorema Egregium! The Euler characteristic is a purely topological property, whereas the Gaussian curvature is purely geometric. The latter requires both a notion of distance and differentiability; the former does not. Nonetheless, they are related to each other.

In the example shown in Figure 1, extended as described above to cover the sphere, there are 8 vertices, 12 edges, and 6 faces, so \begin{equation} \chi(\SSS^2) = 8-12+6 = 2 \end{equation} on the sphere.

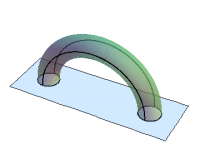
Two simple examples demonstrate the power of the Gauss-Bonnet Theorem. As just computed, the Euler characteristic of a sphere is $2$, and it is easily seen that ($\ref{gb5}$) is satisfied. Adding a handle decreases the Euler characteristic by $2$, as shown in Figure 2: Two faces (the circles) have been removed; two faces (the top and bottom of the tube) and two edges (where the faces meet) have been added. Adding a handle to a sphere yields a torus, whose Euler characteristic turns out to be $0$. Thus, the total Gaussian curvature of a torus must be zero. This is plausible, since the inner half of a donut curves the opposite way from the outer half. One consequence of the Gauss-Bonnet Theorem is that it is not possible to construct a torus so that the Gaussian curvature is everywhere positive!