The reader may have the feeling that two quite different languages are being spoken here. The tilted plane in § {Flux} was treated in essentially the traditional manner found in calculus textbooks, using rectangular coordinates. While the “use what you know” strategy may be somewhat unfamiliar, the basic idea should not be. On the other hand, the examples in § {Highly Symmetric Surfaces} will be quite unfamiliar to most mathematicians, due to their use of adapted basis vectors such as $\rhat$. Mastering these examples helps develop experience looking for symmetry and making geometric arguments. At the same time, not all problems have symmetry!

We argue, however, that the approach being presented here is much more flexible than may appear at first sight. We demonstrate this flexibility by integrating over a paraboloid, the classic example found in calculus textbooks.

We compute the flux of the axially symmetric vector field \begin{equation} \FF = r\,\rhat = x\,\xhat + y\,\yhat \end{equation} “outwards” through the part of the paraboloid $z=r^2$ lying below the plane $z=4$. The first thing we need is the formula for $d\rr$ in cylindrical coordinates, which is a straightforward generalization of (1) of § {Other Coordinate Systems} in polar coordinates, namely \begin{equation} d\rr = dr\,\rhat + r\,d\phi\,\phat + dz\,\zhat \label{dr3} \end{equation}

Figure 1: Chopping up a paraboloid in cylindrical coordinates.

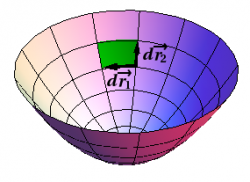
Next, we need two families of curves on the paraboloid; the natural choices are those with $r=\hbox{constant}$ or $\phi=\hbox{constant}$, respectively, as shown in Figure 1. If $r$ is constant, so is $z$, and we have simply \begin{equation} d\rr_1 = r\,d\phi\,\phat \end{equation} If $\phi$ is constant, there will be no $\phat$ term in $d\rr_2$, but we must still use what we know to compute $dz=2r\,dr$, thus obtaining \begin{equation} d\rr_2 = dr\,\rhat + 2r\,dr\,\zhat \end{equation} Taking the cross product leads to (compare (7) of § {Surface Elements}) \begin{equation} d\SS = d\rr_1 \times d\rr_2 = (2r^2\,\rhat - r\zhat) \,dr\,d\phi \end{equation} and at this point we must check that we have chosen the correct orientation. (We have, since the coefficient of $\zhat$ is negative.) The rest is easy: Compute the dot product, determine the limits, and do the integral. This results in \begin{equation} \Sint \FF \cdot d\SS = \int_0^{2\pi} \int_0^2 2r^3 \,dr\,d\phi = 16\pi \end{equation}

It is of course also possible to use rectangular coordinates to determine $d\SS$, choosing curves on the paraboloid $z=x^2+y^2$ with $x=\hbox{constant}$ or $y=\hbox{constant}$. The resulting integral cries out for polar coordinates — which turns it into the same integral as the above.

There is however a significant difference between these two approaches: Drawing the curves on the paraboloid with $r$ or $\phi$ held constant is easy; drawing the curves with $x$ or $y$ held constant is not. Try it!1) The rectangular coordinate approach relies for its geometric intuition on the generic figure found in most textbooks which maps the rectangular “parameter space” into the surface, whereas the cylindrical coordinate approach starts by choosing the geometrically obvious curves in the given surface.