You are here: start » book » guidecontent » dot
Most students first learn the algebraic formula for the dot product in rectangular coordinates, and only then are shown the geometric interpretation. We believe it should be done in the other order. Students tend to remember best the first definition they use; this should not be an algebraic formula devoid of context. The geometric definition is coordinate independent, and therefore conveys invariant properties of the dot product, not just a formula for calculating it.
 Figure 9.1: The dot product is fundamentally a projection.
Figure 9.1: The dot product is fundamentally a projection.
The dot product is fundamentally a projection, as shown in Figure 9.1, which leads to the geometric formula \begin{equation} \vv\cdot\ww = {|\vv| |\ww| \cos\theta} \label{dotgeom} \end{equation} for the dot product of $\vv$ and $\ww$.
An immediate consequence of ($\ref{dotgeom}$) is that the dot product of a vector with itself gives the square of the length, that is \begin{equation} \vv\cdot\vv = |\vv|^2 \end{equation} In particular, taking the “square” of any unit vector yields 1, for example \begin{equation} \ii\cdot\ii = 1 \end{equation} Furthermore, it follows immediately from the geometric definition that two vectors are orthogonal if and only if their dot product vanishes, that is \begin{equation} \vv\perp\ww \Longleftrightarrow \vv\cdot\ww = 0 \end{equation}
If you use orthonormal basis vectors, such as $\{\ii,\jj,\kk\}$ for rectangular coordinates, then the geometric formula reduces to the standard component form of the dot product. For example, if $\vv=v_x\,\ii+v_y\,\jj$ and $\ww=w_x\,\ii+w_y\,\jj$, then 1) \begin{eqnarray} \vv\cdot\ww &=& (v_x\,\ii+v_y\,\jj)\cdot(w_x\,\ii+w_y\,\jj) \nonumber\\ &=& v_x w_x \,\ii\cdot\ii + v_y w_y \,\jj\cdot\jj + v_x w_y \,\ii\cdot\jj + v_y w_x \,\jj\cdot\ii \\ &=& v_x w_x + v_y w_y \nonumber \end{eqnarray} This computation clearly works for any orthonormal basis.
A special case is the dot product of a vector with itself, which reduces to the Pythagorean theorem, for example \begin{equation} \vv\cdot\vv = |\vv|^2 = v_x^2 + v_y^2 \end{equation}
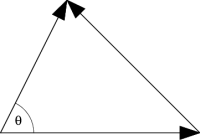 Figure 9.2: The Law of Cosines is just the definition of the dot product.
Figure 9.2: The Law of Cosines is just the definition of the dot product.
What happens if you don't use an orthonormal basis? Consider Figure 9.2, in which $\CC=\BB-\AA$. Then \begin{eqnarray} \CC\cdot\CC &=& (-\AA + \BB) \cdot (-\AA + \BB) \nonumber\\ &=& \AA\cdot\AA + \BB\cdot\BB - 2 \,\AA\cdot\BB \end{eqnarray} or equivalently \begin{equation} |\CC|^2 = |\AA|^2 + |\BB|^2 - 2|\AA||\BB|\cos\theta \end{equation} which is just the Law of Cosines.
A good problem which emphasizes both the geometric and algebraic representations of the dot product is to find the angle between the diagonal of a cube and one of its edges.