As an example of finding the potential due to a continuous charge source, let's calculate the potential the distance $r$ from the center of a uniform line segment of charge with total length $2L$. We will idealize the line segment as infinitely thin and describe it by the constant linear charge density $\lambda$. Because we are chopping a one-dimensional source into little lengths, $d\tau$ reduces to $|d\rr|$. \begin{equation} V(\rr)=\frac{1}{4\pi\epsilon_0}\int \frac{\lambda |d\rr|}{|\rr-\rrp|} \end{equation}

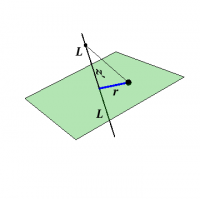
We will choose to work in cylindrical coordinates, centering the line segment on the $z$-axis and will find the potential at a distance $r$ from the origin in the $x$, $y$-plane, as shown in Figure 1. Now, we want to plug in information, using the “use what you know” strategy.

1. The source lies along the $z$-axis at points with coordinates $r'=0$, $\phi'=0$, and $z'$.
2. $|d\rr|$ becomes $dz'$ and the integral runs from $z'=-L$ to $z'=L$.
3. For a voltmeter probe located on the $x$, $y$-plane, we have $z=0$.
4. Because of the cylindrical symmetry, we can choose to evaluate the integral with the voltmeter probe at any $\phi$, so we will choose $\phi=0$ for simplicity. (It is an illuminating exercise to solve the integral for arbitrary $\phi$ and see how the algebra ends up reflecting the cylindrical symmetry.)
5. In cylindrical coordinates (see homework problem: DistanceCurvilinear), the denominator is $\sqrt{r^2+r'^2-2r r' \cos(\phi-\phi')+(z-z')^2}$ which reduces to $\sqrt{r^2+z'^2}$. Alternatively, this result can be obtained directly from a diagram.

Therefore, the integral that we need to perform is \begin{eqnarray} V(r,0,0) &=& \frac{\lambda}{4\pi\epsilon_0}\int_{-L}^{L} \frac{dz'}{\sqrt{r^2+z'^2}} \nonumber\\ &=& \frac{\lambda}{4\pi\epsilon_0} \left.\ln\left(z' + \sqrt{r^2+z'^2}\right)\right|_{-L}^{L} \nonumber\\ &=& \frac{\lambda}{4\pi\epsilon_0} \left(\ln\left(L + \sqrt{r^2+L^2}\right) -\ln\left(-L + \sqrt{r^2+(-L)^2}\right)\right) \nonumber\\ &=& \frac{\lambda}{4\pi\epsilon_0} \ln\left(\frac{L + \sqrt{r^2+L^2}}{-L + \sqrt{r^2+L^2}}\right) \label{vfiniteline} \end{eqnarray} It is a good exercise in series expansions to evaluate this last expression for the case when the voltmeter probe is far away compared to the size of the line segment of charge. What answer do you expect? Is this what you get? What is the quadrupole term? Can you explain this? What about the octopole term?