Recall that for a thin current-carrying loop we have \begin{eqnarray*} \BB(\rr) = {\mu_0\over 4\pi} \int {\II(\rrp)\times(\rr-\rrp)\,ds'\over|\rr-\rrp|^3} = - {\mu_0 I\over 4\pi} \int {(\rr-\rrp)\times d\rrp\over|\rr-\rrp|^3} \end{eqnarray*} For a circular ring of current, we have \begin{eqnarray*} |\rr-\rrp|= \sqrt{r^2 - 2\, rR \cos(\phi-\phi') + R^2 + z^2} \end{eqnarray*}

Make sure you can use this expression to approximate the magnetic field in the various regimes considered in § {Activity: Magnetic Vector Field of a Spinning Ring}. You can check your work using the Mathematica notebook
$\qquad\qquad\qquad\qquad$ Vector Potential of a Spinning Ring
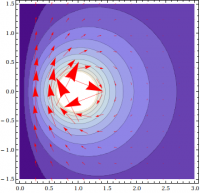
A graphical representation of the result is shown in Figure 1.