Recall that for a thin current-carrying loop we have \begin{eqnarray*} \AA(\rr) = {\mu_0\over 4\pi} \int {\II(\rrp)\,ds'\over|\rr-\rrp|} = {\mu_0\over 4\pi} \int {\lambda(\rrp)\,\vv\,ds'\over|\rr-\rrp|} \end{eqnarray*} For a circular ring of current, we have \begin{eqnarray*} \vv = \frac{2\pi R}{T}\,\phat = \frac{2\pi R}{T}\, \Bigl( -\sin\phi\,\ii + \cos\phi\,\jj \Bigr) \end{eqnarray*} and \begin{eqnarray*} |\rr-\rrp|= \sqrt{r^2 - 2\, rR \cos(\phi-\phi') + R^2 + z^2} \end{eqnarray*}

Make sure you can use these expressions to approximate the vector potential in the various regimes considered in § {Activity: Magnetic Vector Potential of a Spinning Ring}. You can check your work using the Mathematica notebook
$\qquad\qquad\qquad\qquad$ Vector Potential of a Spinning Ring

Recall further that the derivative (gradient) of the scalar potential gives (minus) the electric field, whose derivative (divergence) in turn yields the charge density (divided by $\epsilon_0$). We expect an analogous construction starting with the vector potential.

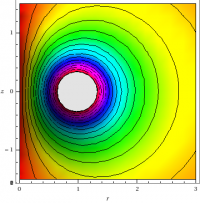
The only derivative we have so far for vector fields is the divergence, so we investigate $\grad\cdot\AA$. Consider the current ring in § {Activity: Magnetic Vector Potential of a Spinning Ring}. We know that $\AA$ takes the form \begin{eqnarray*} \AA = A_\phi(r,z)\,\phat \end{eqnarray*} as shown in Figure 1. What is the flux of $\AA$ out of a small “pineapple”-shaped box? The only surfaces which contribute are those on which $\phi=\hbox{constant}$, and since $A_\phi$ doesn't depend on $\phi$ the flux in one side must equal the flux out the other. We conclude that \begin{eqnarray*} \grad\cdot\AA = 0 \end{eqnarray*} (This is actually a choice: There is considerable freedom in the definition of the vector potential, analogous to adding a constant to the scalar potential. The expression we are using for the vector potential leads to the gauge condition that the divergence of $\AA$ vanish. Put differently, there is no physics in $\grad\cdot\AA$, so we can safely set it to zero.)

So the divergence is not the right kind of derivative here. Actually, we knew that already, since the magnetic field is a vector field, and the divergence is a scalar. Flux doesn't work; what other integrals could we try? Instead of the change in the normal component of $\AA$, let's measure the tangential component. We therefore consider the circulation $\oint\AA\cdot{d\rr}$ of $\AA$ around a closed loop, which leads us to another derivative, namely the curl.

We have seen that the vector potential for a uniform ring of current takes the form \begin{eqnarray*} \AA = A_\phi(r,z)\,\phat \end{eqnarray*} It is easy to argue that the circulation of $\AA$ around a loop in the $rz$-plane is zero, since $\phat$ is perpendicular to the loop. Thus, the $\phat$-component of $\grad\times\AA$ must vanish. Consider now a loop in the $\phi z$-”plane”. The vertical sides again don't contribute, and $\AA$ is strongest near $z=0$. Using the right-hand rule (and assuming positive charge density $\lambda$), this means that the $\rhat$-component of $\grad\times\AA$ must be positive for $z>0$, negative for $z<0$, and zero for $z=0$. (This argument fails along the $z$-axis, where however $\grad\times\AA$ must point in the $\zhat$ direction by symmetry.)

What about the $\zhat$-component? Consider first a small loop around the axis. Since $\AA$ is proportional to $\phat$, the circulation around such a loop is clearly positive. Thus, the $\zhat$-component of $\grad\times\AA$ must be positive everywhere along the axis.

How about away from the axis? Examine a loop in the $xy$-plane, whose sides are $r=\hbox{constant}$ and $\phi=\hbox{constant}$. The radial sides don't contribute, since $\phat$ is perpendicular to them. The inner and outer sides will contribute, and $\AA$ will be stronger on the inner side, which is shorter. So it's not easy to tell what the $z$-component of $\grad\times\AA$ will be.

The vector potential due to a ring of current, in the plane of the ring, with either $r\ll R$ or $r\gg R$, turns out to be \begin{eqnarray*} \AA = \frac{\mu_0 I}{4} \cases{ \frac{r}{R} \left( 1 + \frac38 \frac{r^2}{R^2} + … \right) \phat & ($r\ll R$) \cr \noalign{\smallskip} \frac{R^2}{r^2} \left( 1 + \frac38 \frac{R^2}{r^2} + … \right) \phat & ($r\gg R$) \cr } \end{eqnarray*} Thus, $\AA$ falls off like $\frac{1}{r^2}$ as $r$ goes to infinity, while the length of the circular arcs increases like $r$. Far enough out, the big side loses. Again invoking the right-hand rule, we see that the $z$-component of $\grad\times\AA$ is negative, for $r$ large and $z=0$.

Putting all of this together, it looks like $\grad\times\AA$ loops around the current, in the direction determined by the right-hand rule. This is what we expect for the magnetic field of a current-carrying wire, and it should not surprise you to learn that we can in fact define the magnetic field $\BB$ in general via \begin{eqnarray*} \BB = \grad\times\AA \end{eqnarray*}