Choosing an appropriate coordinate system for a given problem is an important skill. The most frequently used coordinate system is rectangular coordinates, also known as Cartesian coordinates, after René Déscartes. One of the great advantages of rectangular coordinates is that they can be used in any number of dimensions.

In three dimensions, holding any one coordinate fixed yields a surface, which is a plane in the case of rectangular coordinates. A coordinate system can be thought of as a collection of such “constant coordinate” surfaces, and the coordinates of a given point are just the values of those constants on the surfaces which intersect at the point. This is illustrated for rectangular coordinates in Figure 3.

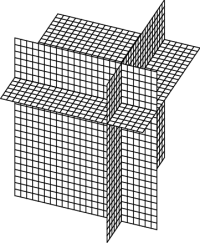Figure 3: The coordinate planes in rectangular coordinates.

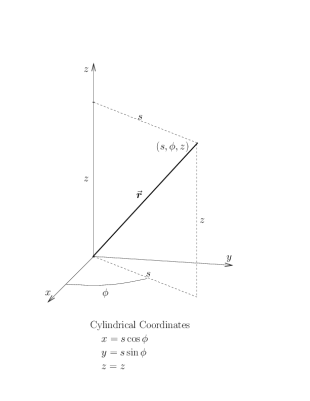
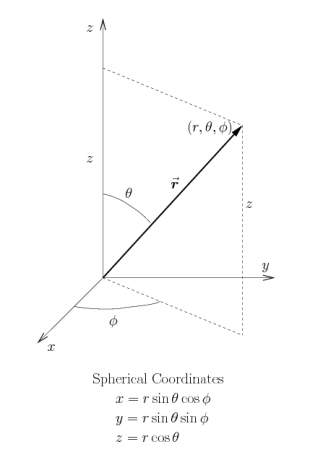
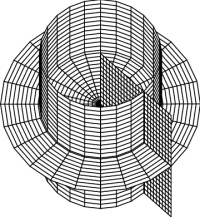
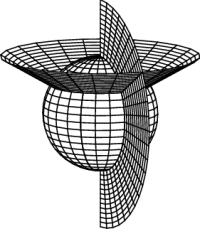
It is often useful, however, to use a coordinate system which shares the symmetry of a given problem — round problems should be done in round coordinates. The two standard “round” coordinate systems are cylindrical coordinates and spherical coordinates, as defined in Figure 4, and whose “constant coordinate” surfaces are shown in Figure 5. Either of these coordinate systems can also be restricted to the $xy$-plane, where they both reduce to polar coordinates. You should be aware that the standard physics conventions for cylindrical and spherical coordinates, used here, differ from the standard (American) math conventions; make sure you understand the difference.