You are here: start » book » math » powertheory
Approximations Using Power Series
Why should you care about power series? Because they allow us to approximate functions to any desired accuracy.
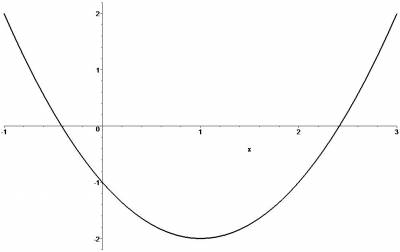
For instance, consider the function $h(x)=-1-2x+x^2$. Draw its graph.
(Notice that we have chosen a particularly simple funciton for this example, a polynomial. Its power series, expanded around the origin, is just the algebraic expression for the function itself. Just by looking at it; you can see that it has only three nonzero terms. Obviously, there is no reason for you to approximate a function this simple. We are using this simple example so that you can think about the separate terms quickly and easily in your head. In § {Finding Power Series Coefficients} and § {Visualizing Power Series Approximations} you have the opportunity to work with the power series for $\sin\theta$, which has an infinite number of terms. You will have many chances to see why power series approximations are useful for more complicated functions later in this text.)
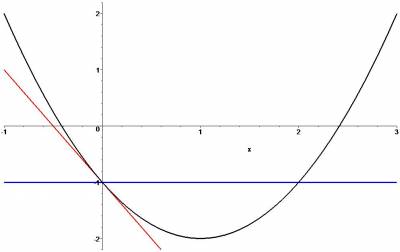
At the origin, The value of the function is $-1$. So, the zeroth order approximation is just the constant function $-1$. It agrees with the value of the function exactly at $x=0$, but otherwise is a pretty lousy approximation. The slope of this graph at $x=0$ is given by the derivative, namely $2$. The linear approximation at the origin to this function is therefore the straight line $y=-1-2x$. Where is the linear approximation of this function a “good” approximation?
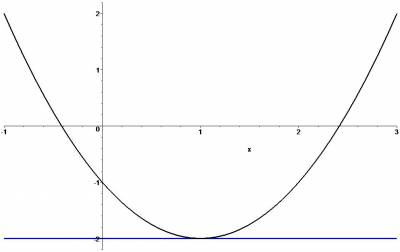
The approximation that we found above, which was a (terminated) series expansion around $x=0$ isn't a very good approximation near $x=1$. We can find a better approximation if we choose to expand around another point, say $x=1$. The expansion of $h$ around $1$ has just two terms, namely $h(x)=-2+(x-1)^2$. The absence of a linear term in this expansion tells us that the graph is horizontal at $x=1$.