The position vector is a unique and very peculiar beast. If you find yourself puzzling about the position vector, read this section. Otherwise, feel free to skip it.

Consider a vector field, such as the electric field due to a point charge. It consists of a vector at each point in space, and is best represented by a vector graph where the tail of each vector is “attached” to the point in space at which the vector field is evaluated.

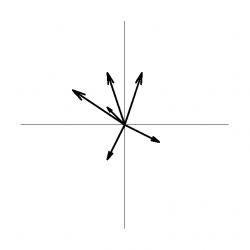
On the other hand, the position vector $\rr$ corresponding to a particular point $P$ in space points from an arbitrary but specific, fixed origin to the point $P$, i.e. its tail is at the origin. If we now let the point $P$ vary all over space, then the position vector becomes a vector field, which we write as $\rr(P)$. There is one vector for each point in space, just as for an ordinary vector field, but now each vector is most naturally represented with its tail at the origin and its head “attached” to the point in space at which the position vector field is being evaluated. See Figure 1a.

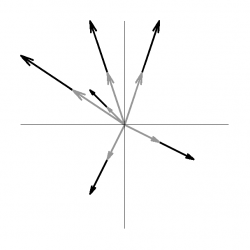
You certainly can represent the position vector by “moving” the tail of each vector in the vector field to the point $P$ and then making the vector point away from the origin and have the magnitude of the vector be the distance of the point $P$ from the origin; see Figure 1b. However, it may make your head hurt to think about it this way if you continue to think of the position vector as telling you, geometrically, how to get from the origin to the point $P$.

In rectangular coordinates, the position vector is given by \begin{equation} \rr=x\,\ii+y\,\jj+z\,\kk \label{position} \end{equation}