In the real world, if you want to find the distance between two objects, you can simply get out your trusty meter stick and measure it. In calculations, it is not quite so simple. First, you must figure out how to describe where the two objects are. To do this, you must choose an origin, and then you must locate the two objects by finding their position vectors $\rr$ and $\rrp$ with respect to that origin. See Figure 1. 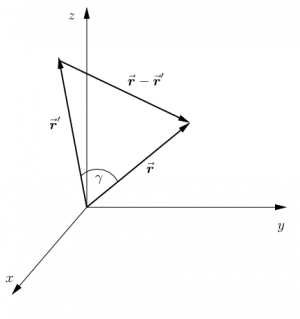Figure 1: The position vectors for two objects and the (vector) difference between them.

Find the vector that points from one of the objects to the other by finding the (vector) difference between the two position vectors and call it, cumbersomely, but not surprisingly, $\rr-\rrp$. Finally, the distance between the two objects is given by the magnitude of this difference vector.

A coordinate-independent description of the distance between the two objects is: \begin{eqnarray*} |\rr-\rrp| &=& \sqrt{(\rr-\rrp)\cdot(\rr-\rrp)} \\ &=& \sqrt{\rr^2+\rrp^2-2\, \rr\, \rrp\, \cos\gamma} \end{eqnarray*} where $\gamma$ is the angle between $\rr$ and $\rrp$. (This result is just the The Law of Cosines.)

To find a coordinate-dependent description, you must choose rectangular coordinates, and find the components of the position vectors with respect to this coordinate system, e.g. $\rr=x\,\ii +y\,\jj +z\,\kk$, yielding: \begin{eqnarray*} |\rr-\rrp| &=& \sqrt{\left((x-x')\,\ii +(y-y')\,\jj +(z-z')\,\kk\right) \cdot \left((x-x')\,\ii +(y-y')\,\jj +(z-z')\,\kk\right)}\\ &=& \sqrt{(x-x')^2+(y-y')^2+(z-z')^2} \end{eqnarray*} Note that this procedure will not work for curvilinear basis vectors. Why not? See § {Wrap-Up: Curvilinear Basis Vectors}.