Wrap-Up: Divergence-Free Vector Fields
Claim: the following conditions are equivalent:
- $\grad\cdot\FF=0$;
- $\int\FF\cdot d\AA$ is independent of surface;
- $\oint\FF\cdot d\AA=0$ for any closed surface;
- $\FF$ is the curl of some other vector field, that is, $\FF=\grad\times\GG$ for some $\GG$.
The magnetic field is always divergence free, since \begin{equation} \BB = \grad\times\AA \end{equation} Thus, \begin{equation} \grad\cdot\BB = 0 \end{equation} which is one of Maxwell's equations.
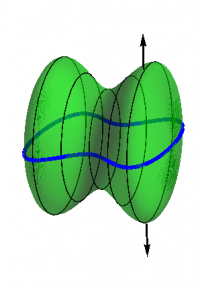
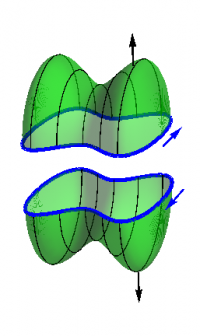
Since any closed surface can be broken up into two surfaces with the same boundary curve, but with opposite orientations, as shown in Figures 1a and 1b, it is easy to see that $2\Leftrightarrow3$. More explicitly, if $S_1$ and $S_2$ are any two surfaces with boundary curve $C$, then \begin{equation} \Int_{S_1} \FF\cdot d\AA = \Int_{S_2} \FF\cdot d\AA \end{equation} where both fluxes are taken in the upward direction. If $S$ is the combined surface $S_1+S_2$, then \begin{equation} \oint\limits_S \FF\cdot d\AA = \Int_{S_1} \FF\cdot d\AA - \Int_{S_2} \FF\cdot d\AA = 0 \end{equation} since the flux on the left is in the outward direction, which shows $2\Rightarrow3$. To show $3\Rightarrow2$, start with any closed surface $S$, and break it up into two surfaces $S_1$ and $S_2$, then run the argument backwards.
To show that $4\Rightarrow2$, use Stokes' Theorem, which implies that \begin{equation} \Int_S \FF\cdot d\AA = \Int_S (\grad\times\GG)\cdot d\AA = \oint\limits_C \GG\cdot d\rr \end{equation} for any surface with boundary curve $C$. A similar argument for a closed surface, whose boundary is empty, establishes $4\Rightarrow3$ directly.
The equivalence of $1$ and $3$ follows from the Divergence Theorem, which says \begin{equation} \int\grad\cdot\FF \>d\tau = \oint \FF\cdot d\AA \end{equation} from which $1\Rightarrow3$ follows immediately. To show $3\Rightarrow1$, one must use the fact that the right-hand side of this equation now vanishes by assumption for any region whose boundary is the given surface, which forces the integrand, and not merely the integral, on the left-hand side to vanish.
To show that $4\Rightarrow1$, one can compute the curl of an unknown vector field $\GG$ in rectangular coordinates, then take the divergence, and use the fact that mixed partial derivatives are equal regardless of order. As discussed in § {Second Derivatives}, a more geometric argument combines the above arguments that $4\Rightarrow3\Rightarrow1$, thus showing directly that \begin{equation} \grad\cdot(\grad\times\GG) = 0 \end{equation} for any vector field $\GG$.
Finally, to argue that $2\Rightarrow4$, one can construct $\GG$ explicitly by integrating the components of $\FF$, although the argument is more subtle than for the case of finding a potential function for a curl-free vector field. Alternatively, one can reason by analogy with the Biot-Savart Law, which expresses $\BB$ in terms of $\JJ$, noting that $\grad\times\BB=\mu_0\JJ$.