Claim: the following conditions are equivalent:

1. $\grad\times\FF=\zero$;
2. $\int\FF\cdot d\rr$ is independent of path;
3. $\oint\limits\FF\cdot d\rr=0$ for any closed path;
4. $\FF$ is the gradient of some scalar field, that is, $\FF=\grad f$ for some $f$.

The electric field is always curl free, since \begin{equation} \EE = -\grad V \end{equation} Thus, \begin{equation} \grad\times\EE = \zero \end{equation} which is one of Maxwell's equations.

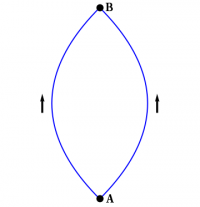
Since any closed path can be broken up into two paths between the same endpoints, but with opposite orientations, it is easy to see that $2\Leftrightarrow3$. More explicitly, if $C_1$ and $C_2$ are any two paths from $A$ to $B$, as shown in Figure1, then \begin{equation} \Int_{C_1} \FF\cdot d\rr = \Int_{C_2} \FF\cdot d\rr = \Int_A^B \FF\cdot d\rr \end{equation} and if $C$ is the path from $A$ to $B$ along $C_1$, then back to $A$ along $C_2$, then \begin{equation} \oint\limits_C \FF\cdot d\rr = \Int_{C_1} \FF\cdot d\rr - \Int_{C_2} \FF\cdot d\rr = 0 \end{equation} which shows $2\Rightarrow3$. To show $3\Rightarrow2$, start with any closed path $C$, and break it up into two paths $C_1$ and $C_2$, then run the argument backwards.

To show that $4\Rightarrow2$, use the Master Formula \begin{equation} df = \grad f\cdot d\rr \end{equation} which implies that \begin{equation} \Int_A^B \FF\cdot d\rr = \Int_A^B \grad f\cdot d\rr = \Int_A^B df = f \bigg|_A^B \end{equation} along any path from $A$ to $B$. A similar argument with $B=A$ establishes $4\Rightarrow3$ directly.

The equivalence of $1$ and $3$ follows from Stokes' Theorem, which says \begin{equation} \int(\grad\times\FF)\cdot d\AA = \oint \FF\cdot d\rr \end{equation} from which $1\Rightarrow3$ follows immediately. To show $3\Rightarrow1$, one must use the fact that the right-hand side of this equation now vanishes by assumption for any surface whose boundary is the given curve, which forces the integrand, and not merely the integral, on the left-hand side to vanish.

To show that $4\Rightarrow1$, one can compute the gradient of an unknown function $f$ in rectangular coordinates, then take the curl, and use the fact that mixed partial derivatives are equal regardless of order. As discussed in §Second Derivatives, a more geometric argument combines the above arguments that $4\Rightarrow3\Rightarrow1$, thus showing directly that \begin{equation} \grad\times\grad f = \zero \end{equation} for any function $f$.

Finally, to argue that $2\Rightarrow4$, one constructs $f$ explicitly by integrating $\FF\cdot d\rr$ from some fixed starting point; the value of the integral depends only on the endpoint by assumption. It is then possible to compute the gradient of this function explicitly, and show that this derivative of an integral does indeed yield what you started with, in this case the vector field $\FF$.

Alternatively, the Murder Mystery Method can be used to find the potential function $f$; path independence guarantees that the consistency check will succeed.