If the limits are not constant, double integrals can still be evaluated in either order; the answer is still the same, although the limits and actual integrals evaluated may not be, as we now demonstrate.

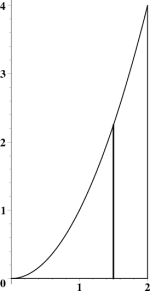
Figure 2: Chopping the region under a parabola vertically.
Figure 3: Chopping the region under a parabola horizontally.

Consider the classic example of finding the area under the graph of $y=x^2$ between $x=0$ and $x=2$. Yes, this can be done as a single integral, but let's do it as a double integral. The most natural chopping is to start with vertical lines, as shown in Figure 2. We have \begin{eqnarray} A &=& \int dA \nonumber\\ &=& \Int_0^2 \left( \Int_0^{x^2} \,dy \right) \,dx \nonumber\\ &=& \Int_0^2 x^2 \,dx = \frac83 \end{eqnarray} Note first of all that the last integral is just the one you'd get by starting with the single integral for the area under the graph; this is not a coincidence. Note also the limits on the two integrals. The limits on $x$ are easy, but where did the “$x^2$” limit on $y$ come from? That's easy; look again at Figure 2. The typical vertical line starts at $y=0$ and goes to $y=x^2$. Since $x$ varies later, when doing the outer integral, we have to keep track of this variable height.

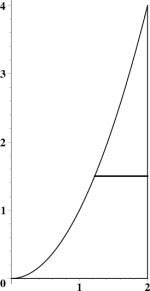
To illustrate these ideas, let's do the integral again, but chop first in the $x$ direction, as shown in Figure 3. Now we must do the integrals in the other order — and the limits are different. We have \begin{equation} A = \int dA = \Int_0^4 \left( \Int_{\sqrt{y}}^2 \,dx \right) \,dy = \Int_0^4 (2-\sqrt{y}) \,dy = \left( 2y - \frac{y^{3/2}}{\frac{3}{2}} \right) \Bigg|_0^4 = \frac83 \end{equation} Make sure you understand where these limits come from! It is often the case that such integrals are much easier to evaluate in one order than the other.

It is a good idea to always draw a typical “first slice”, as shown in the figures, before determining the limits and evaluating the integral.

What about triple integrals? Just as for double integrals, it is often easiest conceptually to do the vertical integration first. Thus, first slice the region into vertical lines from top to bottom (integrate with respect to $z$), then add up the result into vertical slices like pieces of bread (integrate with respect to $y$), then finally assemble the slices into the full region (integrate with respect to $x$).

For example, the volume of a sphere of radius $R$ can be computed in rectangular coordinates as \begin{equation} V = \Int_{-R}^R \left( \Int_{-\sqrt{R^2-y^2}}^{\sqrt{R^2-y^2}} \left( \Int_{-\sqrt{R^2-x^2-y^2}}^{\sqrt{R^2-x^2-y^2}} \,dz\right)\,dy\right)\,dx \end{equation}

This is not the easiest way to find the volume of a sphere. (Can you think of a better way?) But you should make sure both that you understand where all the limits come from, and that you could evaluate all three integrals if necessary. (HINT: One of them is easy.)