A basis vector of the form $\widehat{coordinate}$ is the unit vector that points in the direction in which $coordinate$ is changing. For example, $\xhat$ is the unit vector that points in the direction that $x$ is changing.
Figure 1: The definition of cylindrical and spherical coordinates, showing the associated basis vectors.In § {Activity: Basis Vectors}, you should have learned the following things.
- Figure 1 shows the directions that you should have pointed if you were standing at a particular position in the room. Make sure that the directions in which you pointed agree with the directions shown in the figure. In particular, $\that$ should point generally downward (for $z>0$) since $\theta$ is measured from the positive $z$-axis.
- The basis vectors are vectors, that is, they are straight arrows in space, even when they correspond to coordinates that are angles. Your arm should therefore have been straight, no matter which basis vector you were representing.
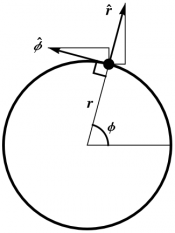
- Although the basis vectors that correspond to rectangular coordinates $x$, $y$, and $z$ are constants, and point in the same direction at each point in space, most of the basis vectors that correspond to cylindrical and spherical coordinates point in different directions at different points in space. Figure 2 shows the construction of the polar (or cylindrical) basis vectors $\rhat$ and $\phat$ at a particular point in a way that details how the direction of these vectors depends on the coordinate $\phi$ of the point.
These curvilinear basis vectors are just as good, as basis vectors, as the rectangular ones. Therefore, you can expand all of the vectors at a given point in terms of the basis vectors associated with that point, e.g. $$\vv=v_r\rhat+v_{\theta}\that+v_{\phi}\phat$$ Be careful, though. When using basis vectors adapted to curvilinear coordinates in sums and differences (including integrals), it is essential to remember that these basis vectors are not constant. For example, if you try to add two vectors that are expanded in terms of the basis vectors appropriate to two different points, e.g. $\{\rhat_1,\that_1,\phat_1\}$ and $\{\rhat_2,\that_2,\phat_2\}$, you cannot simply add the components: \begin{eqnarray} \vv_1+\ww_2 &=&(v_r\rhat_1+v_{\theta}\that_1+v_{\phi}\phat_1) +(w_r\rhat_2+w_{\theta}\that_2+w_{\phi}\phat_2)\\ &\ne&(v_r+w_r)\rhat+(v_{\theta}+w_{\theta})\that+(v_{\phi}+w_{\phi})\phat\nonumber \end{eqnarray} Similarly, later in this text, when we discuss taking various derivatives of vector fields, we will need to show how to take the derivatives of these curvilinear basis vectors.
The basis vectors adapted to a single coordinate form a simple example of the geometrical notion of a vector field, that is, a vector at every point in space. Figure 3 shows these vector fields in polar coordinates. Vector fields are discussed further in § {Vector Fields},
Figure 3: The polar basis vector fields $\rhat$ and $\phat$.