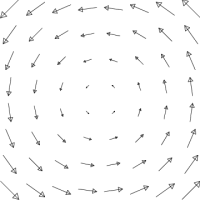
Visualizing Conservative Vector Fields
Which of the above vector fields is conservative?
It is usually easy to determine that a given vector field is not conservative: Simply find a closed path around which the circulation of the vector field doesn't vanish. But how does one show that a given vector field is conservative? Consider the figures below. It is easy to see that the figure on the right is not conservative. But what about the one on the left?
A conservative vector field is the gradient of a potential function. The “equipotential” surfaces, on which the potential function is constant, form a topographic map for the potential function, and the gradient is then the slope field on this topo map. This analogy is exact for functions of two variables; conservative vector fields are those which correspond to topo maps.
This provides a graphical technique for determining whether a given vector field (in two dimensions) is conservative: Try to draw its topo map. Let's give it a try. Yes indeed, the vector field on the left below appears to be conservative, and the one on the right is not. What are the rules?
- The level curves must be everywhere perpendicular to the vector field.
- The level curves must be close together where the magnitude of the vector is large.
- Level curves corresponding to different values may not intersect.
Here are two more examples. Which of these vector fields is conservative?
Try drawing boxes:
Try drawing level curves:
What can you conclude?