Prerequisites
Polar Coordinates
Polar coordinates are useful for situations with circular symmetry in the plane.
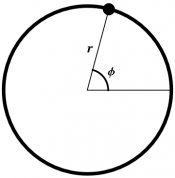
The polar coordinates ($r$,$\phi$) of a point $P$ give the distance $r$ that from the given origin to $P$, together with the angle $\phi$ from the positive $x$-axis to $P$, as shown in Figure 1. You will also see this angle called $\theta$ instead of $\phi$; we use $\phi$ to agree with our conventions for (cylindrical and) spherical coordinates.
It is important to remember that the angle $\phi$ does not measure distance; it has the wrong dimensions. Angles (in radians) are defined as the ratio of arclength to radius on the circle, so the arclength from the positive $x$-axis to $P$ along the circle shown in the figure is just $r\phi$.