Optimization
Before considering functions of several variables, let us first review how to find maxima and minima for functions of one variable. Recall that a local max/min can only occur at a critical point, where the derivative either vanishes or is undefined. The second derivative test can help to determine whether a critical point is a max or a min: If the second derivative is positive or negative, then the graph is concave up or down, respectively, and the critical point is a local min or a local max, respectively. However, if the second derivative vanishes, anything can happen.
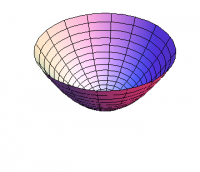
Now imagine the graph of a function of two variables. At a local minimum, you would expect the slope to be zero, and the graph to be concave up in all directions. A typical example would be \[ f(x,y) = x^2 + y^2 \] at the origin, as shown in Figure 1.
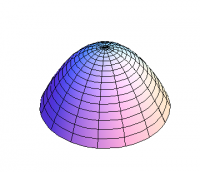
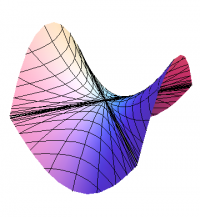
Similarly, at a local maximum, the slope would again be zero but the graph would be concave down in all directions; a typical example would be \[ g(x,y) = -x^2 - y^2 \] again at the origin, as shown in Figure 2. But now there is another possibility. Consider the function \[ h(x,y) = x^2 - y^2 \] whose graph still has slope zero at the origin, but which is concave up in the $x$-direction, yet concave down in the $y$-direction; this is a saddle point, as shown in Figure 3.
Motivated by the above examples, a critical point of a function $f$ of several variables occurs where all of the partial derivatives of $f$ either vanish or are undefined.
Critical points of a function $f(x,y)$ of two variables can be classified using the second derivative test, which now takes the following form. Let \begin{eqnarray} D &=& \frac{\partial^2 f}{\partial x^2}\frac{\partial^2 f}{\partial y^2} - \left(\frac{\partial^2 f}{\partial x\partial y}\right)^2 \\ A &=& \frac{\partial^2 f}{\partial x^2} \end{eqnarray} evaluated at a critical point $P=(a,b)$. Then
- If $D>0$ and $A>0$, then $f(a,b)$ is a local min.
- If $D>0$ and $A<0$, then $f(a,b)$ is a local max.
- If $D<0$, then there is a saddle point at $P$.
- If $D=0$, anything can happen.
Optimization problems typically seek a global max/min, rather than a local max/min. Just as for functions of one variable, in addition to finding the critical points, one must also examine the boundary. Thus, to optimize a function $f$ of several variables, one must:
- Find the critical points.
- Find any critical points of the function restricted to the boundary.
- Evaluate $f$ at each of these points to find the global max/min.
As an example, consider the function $f(x,y)=xy$. Where are the critical points? Where the partial derivatives of $f$ vanish. We have \begin{equation} \Partial{f}{x} = y ;\qquad \Partial{f}{y} = x \end{equation} so the only critical point occurs where $x=0=y$, that is, at the origin. We compute second derivatives and evaluate them at the origin, obtaining \begin{equation} \frac{\partial^2 f}{\partial x^2}\Bigg|_{(0,0)} = 0 = \frac{\partial^2 f}{\partial y^2}\Bigg|_{(0,0)} ; \qquad \frac{\partial^2 f}{\partial x\partial y}\Bigg|_{(0,0)} = 1 \end{equation} so that in this case \begin{equation} D = 0 - 1 = -1 < 0 \end{equation} which implies that $(0,0)$ is a saddle point of $f$.