Prerequisites
The Divergence Theorem
The total flux of the electric field out through a small rectangular box is \begin{eqnarray*} {\rm flux} = \sum_{\rm box} \EE \cdot d\AA = \grad\cdot\EE \> dV \end{eqnarray*}
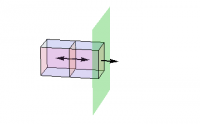
But any closed region can be filled with such boxes, as shown in Figure 1a. Furthermore, the flux out of such a region is just the sum of the flux out of each of the smaller boxes, since the net flux through any common face will be zero (because adjacent boxes have opposite notions of “out of”), as indicated schematically in Figure 1b. Thus, the total flux out of any closed box is given by \begin{eqnarray*} \Int_{\rm box} \EE \cdot d\AA = \Int_{\rm inside} \!\! \grad\cdot\EE \>\> dV \end{eqnarray*} This is the Divergence Theorem.