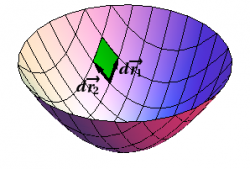
General Surface Elements
Since surfaces are two-dimensional, chopping up a surface is usually done by drawing two families of curves on the surface. Then you can compute $d\rr$ on each family and take the cross product, to get the vector surface element in the form \begin{equation} d\SS = d\rr_1 \times d\rr_2 \label{Surface} \end{equation} In order to determine the area of the vector surface element, we need the magnitude of this expression, which is \begin{equation} \dS = |d\SS| = |d\rr_1\times d\rr_2| \label{Scalar} \end{equation} and which is called the (scalar) surface element. This should remind you of the corresponding expression for line integrals, namely $ds=|d\rr|$.
We illustrate this technique by computing the surface element for the paraboloid given by $z=x^2+y^2$, as shown in Figure 1, with the two families of curves corresponding to $\{x=\hbox{const}\}$ and $\{y=\hbox{const}\}$. We start with the basic formula for the vector differential $d\rr$, namely \begin{equation} d\rr = dx\,\xhat + dy\,\yhat + dz\,\zhat \end{equation} What do you know? The expression for $z$ leads to \begin{equation} dz = 2x\,dx + 2y\,dy \end{equation} In rectangular coordinates, it is natural to consider infinitesimal displacements in the $x$ and $y$ directions. In the $x$ direction, $y$ is constant, so $dy=0$, and we obtain \begin{equation} d\rr_1 = dx\,\xhat + 2x\,dx\,\zhat = (\xhat + 2x\,\zhat)\, dx \end{equation} Similarly, in the $y$ direction, $dx=0$, which leads to \begin{equation} d\rr_2 = dy\,\yhat + 2y\,dy\,\zhat = (\yhat + 2y\,\zhat)\, dy \end{equation} Putting this together, we obtain \begin{eqnarray} d\SS = d\rr_1 \times d\rr_2 &=& (\xhat + 2x\,\zhat) \times (\yhat + 2y\,\zhat) \,dx\,dy \nonumber\\ &=& (-2x\,\xhat - 2y\,\yhat + \zhat) \,dx\,dy \label{parabolaR} \end{eqnarray} for the vector surface element, and \begin{equation} \dS = \left|{-}2x\,\xhat - 2y\,\yhat + \zhat\right| \,dx\,dy = \sqrt{1+4x^2+4y^2}\,dx\,dy \end{equation} for the scalar surface element. Can you repeat this computation in cylindrical coordinates? (See § {Less Symmetric Surfaces} for the answer.)
This construction emphasizes that “area” is really a vector, whose direction is perpendicular to the surface, and whose magnitude is the area. Note that there are always two choices for the direction; choosing one determines the orientation of the surface.
When using ($\ref{Surface}$) and ($\ref{Scalar}$), it doesn't matter how you chop up the surface. It is of course possible to get the opposite orientation, for instance by interchanging the roles of $d\rr_1$ and $d\rr_2$. Rather than worrying too much about getting the “right” orientation from the beginning, it is usually simpler to check after you've calculated $dSS$ whether the orientations you've got agrees with the requirements of the problem. If not, insert a minus sign.
Just as a curve is a 1-dimensional set of points, a surface is 2-dimensional. When computing line integrals, it was necessary to write everything in terms of a single parameter before integrating. Similarly, for surface integrals you must write everything, including the limits of integration, in terms of exactly two parameters before starting to integrate.
Finally, a word about notation. You will often see $dS$ instead of $dA$, and $d\vec S$ instead of $d\SS$; most authors use $dA$ in the $xy$-plane.