Chain Rule via Differential Tree Diagrams
Suppose $f=f(x,y)$. Then of course \begin{equation} df = \left(\Partial{f}{x}\right)_y dx + \left(\Partial{f}{y}\right)_x dy \end{equation} where the subscripts keep track of which variables are being held constant when taking partial derivatives. If $x=x(u,v)$, $y=y(u,v)$, then \begin{equation} dx = \left(\Partial{x}{u}\right)_v du + \left(\Partial{x}{v}\right)_u dv \end{equation} with a similar expression holding for $dy$. Combining these expressions and rearranging terms, we obtain \begin{equation} df = \left( \left(\Partial{f}{x}\right)_y \left(\Partial{x}{u}\right)_v + \left(\Partial{f}{y}\right)_x \left(\Partial{y}{u}\right)_v \right) du \\ + \left( \left(\Partial{f}{x}\right)_y \left(\Partial{x}{v}\right)_u + \left(\Partial{f}{y}\right)_x \left(\Partial{y}{v}\right)_u \right) dv \end{equation}
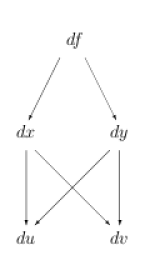
But we also know that \begin{equation} df = \left(\Partial{f}{u}\right)_v du + \left(\Partial{f}{v}\right)_u dv \end{equation} Comparing these two expressions for $df$ and setting $v=\hbox{constant}$, we obtain \begin{equation} \left(\Partial{f}{u}\right)_v = \left(\Partial{f}{x}\right)_y \left(\Partial{x}{u}\right)_v + \left(\Partial{f}{y}\right)_x \left(\Partial{y}{u}\right)_v \label{fu} \end{equation} with a similar expression holding for the derivative of $f$ with respect to $v$.
An easy way to remember such formulas is to use a tree diagram, as shown in Figure 1a above. To use a tree diagram, determine which derivative you want to take, in this case the derivative of $f$ with respect to $u$. Thus, you need to express $df$ in terms of $du$. Now follow all possible paths from $df$ to $du$, with each arrow corresponding to an expansion of the “top” quantity in terms of the “bottom” quantity, that is, to a partial derivative, where the variable(s) not pointed to by the arrow are to be held constant.
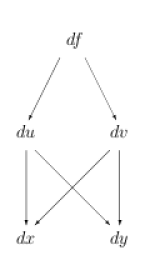
However, one often wants to know how to express the derivatives of $f$ with respect to $x$ and $y$ in terms of its derivatives with respect to $u$ and $v$, rather than the other way around. The argument in this case is the same, with the roles of ($x$,$y$) and ($u$,$v$) reversed, as in the tree diagram in Figure 1b above. This results in \begin{equation} \left(\Partial{f}{x}\right)_y = \left(\Partial{f}{u}\right)_v \left(\Partial{u}{x}\right)_y + \left(\Partial{f}{v}\right)_u \left(\Partial{v}{x}\right)_y \label{fx} \end{equation} with a similar expression for the derivative of $f$ with respect to $y$. When comparing ($\ref{fx}$) with ($\ref{fu}$), it is important to realize that $\left(\Partial{x}{u}\right)_v$ and $\left(\Partial{u}{x}\right)_y$ are not necessarily reciprocals of each other. 1)
Finally, it is possible to reinterpret ($\ref{fx}$) as a statement about derivative operators, rather than derivatives, simply by removing $f$. Thus, \begin{equation} \left(\Partial{}{x}\right)_y = \left(\Partial{u}{x}\right)_y \left(\Partial{}{u}\right)_v + \left(\Partial{v}{x}\right)_y \left(\Partial{}{v}\right)_u \end{equation} where we have reordered the terms slightly. When using such expressions, you will often need to express the derivatives on the RHS in terms of $u$ and $v$ alone, rather than in terms of $x$ and $y$. Having done so, it is possible to use these expressions to determine higher-order derivative operators as well, such as the Laplacian.