It can be useful to consider divergence in two dimensions, rather than three, since such vector fields are easier to visualize; the price is that such vector fields are usually less physical. In this context, divergence can be defined as the flux per unit area through a small (2-dimensional) box.

Figure 6.1: An axially symmetric vector field with vanishing flux.

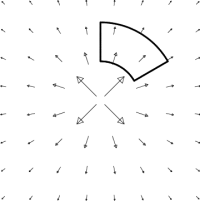
For example, for the vector field \begin{equation} \FF = \frac{x\,\ii+y\,\jj}{(x^2+y^2)} = \frac{\rhat}{r} \end{equation} which is axially symmetric, one should use a box adapted to polar coordinates, as shown in Figure 6.1. The box is pie-shaped, with the pointy end cut off in a circular arc (i.e. a big circular arc, a smaller circular arc closer to the origin, and two radial line segments that join the arcs). The magnitude of the vector field falls off like $\frac{1}{r}$ as you move radially outward from the origin, so one's first guess might be that the net flux is negative, that is, there is more flux into the box at the smaller radius than out of the box at the larger radius (and none through the sides). However, it turns out that the longer length of the latter side arclength exactly cancels this effect, since arclength is proportional to radius; the net flux is zero.

In three dimensions, the corresponding example is \begin{equation} \GG = \frac{x\,\ii+y\,\jj+y\,\kk}{(x^2+y^2+z^2)^{\frac32}} = \frac{\rhat}{\,r^2} \end{equation} which is spherically symmetric, and which falls off like $\frac{1}{r^2}$. The appropriate box for visualizing divergence is now a piece of a spherical shell, and the flux is only nonzero for the inner and outer faces of the box. The larger area of the outer face again exactly cancels the smaller magnitude of the vector field; the net flux is zero.

This only happens, of course, if the vector field falls off in exactly the right way; changing the power of $r$ in the denominator would lead to a nonzero flux. Remarkably, it is exactly the balanced case which occurs in the universe, both in electrostatics and in gravity. The electric field due to a point charge $q$ is \begin{equation} \EE = \frac{1}{4\pi\epsilon_0} \frac{q\,\rhat}{r^2} \end{equation} and the gravitational field due to a point mass $m$ is \begin{equation} \gv = G \, \frac{m\,\rhat}{r^2} \end{equation} where $\epsilon_0$ and $G$ are physical constants (which depend on the choice of units).

Furthermore, the laws of physics show that this same kind of detailed cancellation occurs whenever there is no charge density ($\rho_e=0$) or mass density ($\rho_m=0$). One of Maxwell's equations for electrostatics is \begin{equation} \grad\cdot\EE = \frac{1}{\epsilon_0} \rho_e \end{equation} and similarly for gravity \begin{equation} \grad\cdot\gv = 4\pi G \rho_m \end{equation} There may well be complicated electric fields in some region of space, but if there is no charge density at a given point, the divergence of the electric field will be zero there, so that the net flux of the electric field through any small box around that point will be zero. A similar statement can be made for the gravitational field.

This geometric fact leads to the convenient notion of field lines. If one draws throughout space a number of lines which is everywhere proportional to the amount of flux per unit area, then these lines can only begin and end at points where the divergence is nonzero, that is, where sources, such as charges or masses, exist.

Curl is circulation per unit area. More precisely, the circulation around a small loop, divided by the area of the loop, gives a good approximation to the component of the curl perpendicular to the loop. A good way to visualize circulation is to ask whether a paddle wheel (whose “handle” is perpendicular to the loop) will spin.

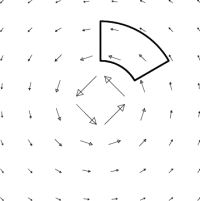
In practice, one often considers loops in coordinate planes such as the $xy$-plane, for which the circulation per unit area yields the $\kk$-component of the curl. For example, consider the vector field \begin{equation} \KK = \frac{-y\,\ii+x\,\jj}{(x^2+y^2)} = \frac{\phat}{r} \end{equation}

It seems clear that a paddle wheel at the origin will spin. If you put the paddle wheel in somewhere else, then there are long arrows pushing on the paddle closest to the origin and short arrows pushing on the paddle furthest from the origin, so one might expect the paddle wheel to spin. But there is a sense in which there are “more” arrows further from the origin. So more short arrows cancel fewer long arrows. It is hard with the paddle wheel picture to see how this goes quantitatively, so let's try to compute the circulation.

Figure 6.2: An axially symmetric vector field with vanishing curl.

For this problem, it is easiest to use a pie-shaped loop, with the pointy end cut off as before, as shown in Figure 6.2. Now, $\KK$ is perpendicular to the radial line segments, which therefore don't contribute to the circulation. On each of the circular arcs, $\KK$ has constant magnitude and is parallel to the curve, so the line integral for these parts is just $|\KK|$ times the length of the arc. If the vector field falls off fast enough (magnitude gets smaller further from the origin), then the contribution from the big arc (smaller $|\KK|$, but larger arclength) is smaller than the contribution from the small arc (larger $|\KK|$, but smaller arclength) and the ($\kk$-component of the) curl will be negative. If the falloff is too slow, then the contribution from the larger arc will dominate and the ($\kk$-component of the) curl will be positive. For the particular falloff in this example, it turns out the contributions from the two arcs exactly cancel and the curl is precisely zero everywhere except at the origin.

Remarkably, the universe tends to pick out those cases which are balanced in this way. The magnetic field outside a current carrying wire is given by \begin{equation} \BB = {\mu_0 I\over2\pi} \frac{\phat}{r} \end{equation} where $\mu_0$ is a physical constant and $I$ denotes the current.

The laws of physics again show that this same kind of detailed cancellation occurs whenever there is no current. Another of Maxwell's equations is \begin{equation} \grad\times\BB = \mu_0 \JJ \end{equation} where $\JJ$ is the current density. There may well be complicated magnetic fields in some region of space, but if there is no current density at a given point, the curl of the magnetic field will be zero there, so that the net circulation of the magnetic field around any small loop around that point will be zero.