Rectangular Coordinates
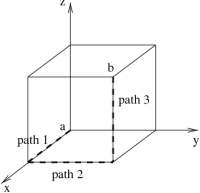
The arbitrary infinitesimal displacement vector in Cartesian coordinates is: $$d\rr=dx\,\xhat + dy\,\yhat +dz\,\zhat$$ Given the cube shown below, find $d\rr$ on each of the three paths, leading from $a$ to $b$.
Path 1: $d\rr=$
Path 2: $d\rr=$
Path 3: $d\rr=$
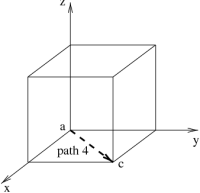
The first expression above for $d\rr$ is valid for any path in rectangular coordinates. Find the appropriate expression for $d\rr$ for the path which goes directly from $a$ to $c$ as drawn below.
Path 4: $d\rr=$
However, Cartesian coordinates would be a poor choice to describe a path on a cylindrically or spherically shaped surface. Next we will find an appropriate expression in these cases.
Cylindrical Coordinates
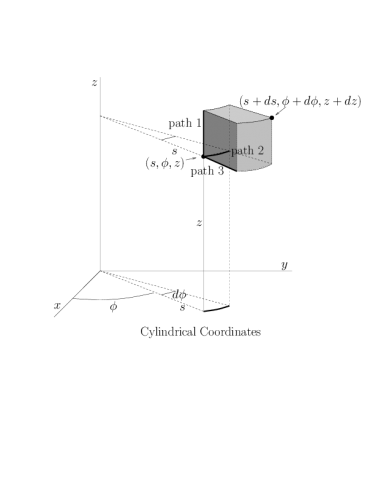
You will now derive the general form for $d\rr$ in cylindrical coordinates by determining $d\rr$ along the specific paths below.
Note that an infinitesimal element of length in the $\rhat$ direction is simply $dr$, just as an infinitesimal element of length in the $\xhat$ direction is $dx$. But, an infinitesimal element of length in the $\phat$ direction is not just $d\phi$, since this would be an angle and does not have the units of length.
Geometrically determine the length of the three paths leading from $a$ to $b$ and write these lengths in the corresponding boxes on the diagram.
Now, remembering that $d\rr$ has both magnitude and direction, write down below the infinitesimal displacement vector $d\rr$ along the three paths from $a$ to $b$. Notice that, along any of these three paths, only one coordinate $r$, $\phi$, or $z$ is changing at a time (i.e. along path 1, $dz\ne0$, but $d\phi=0$ and $dr=0$).
Path 1: $d\rr=$
Path 2: $d\rr=$
Path 3: $d\rr=$
If all three coordinates are allowed to change simultaneously, by an infinitesimal amount, we could write this $d\rr$ for any path as:
$d\rr$=
This is the general line element in cylindrical coordinates.
Spherical Coordinates
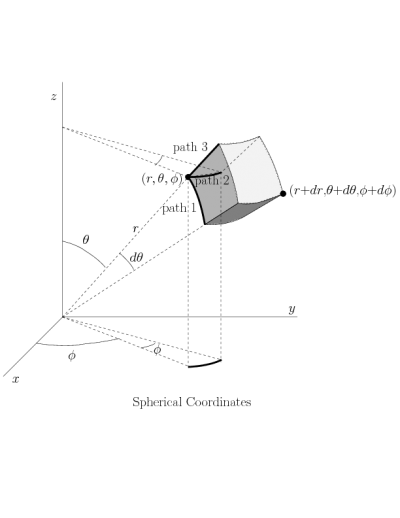
You will now derive the general form for $d\rr$ in spherical coordinates by determining $d\rr$ along the specific paths below. As in the cylindrical case, note that an infinitesimal element of length in the $\that$ or $\phat$ direction is not just $d\theta$ or $d\phi$. You will need to be more careful. Geometrically determine the length of the three paths leading from $a$ to $b$ and write these lengths in the corresponding boxes on the diagram. Now, remembering that $d\rr$ has both magnitude and direction, write down below the infinitesimal displacement vector $d\rr$ along the three paths from $a$ to $b$. Notice that, along any of these three paths, only one coordinate $r$, $\theta$, or $\phi$ is changing at a time (i.e. along path 1, $d\theta\ne0$, but $dr=0$ and $d\phi=0$).
Path 1: $d\rr=$
Path 2: $d\rr=$
(Be careful, this is the tricky one.)
Path 3: $d\rr=$
If all 3 coordinates are allowed to change simultaneously, by an infinitesimal amount, we could write this $d\rr$ for any path as:
$d\rr$=
This is the general line element in spherical coordinates.