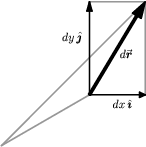
Figure 3.1: The infinitesimal displacement vector $d\rr$ along a curve, shown in an
“infinite magnifying glass”. In this and subsequent figures, artistic
license has been taken in the overall scale and the location of the origin
in order to make a pedagogical point.
Figure 3.1: The infinitesimal displacement vector $d\rr$ along a curve, shown in an
“infinite magnifying glass”. In this and subsequent figures, artistic
license has been taken in the overall scale and the location of the origin
in order to make a pedagogical point.
The position vector 1) \begin{equation} \rr=x\,\ii+y\,\jj+z\,\kk \end{equation} describes the location of the point $(x,y,z)$ in rectangular coordinates. It is instructive to draw a picture of the small change $\Delta\rr=\Delta x\,\ii + \Delta y\,\jj + \Delta z\,\kk$ in the position vector between nearby points. Try it! This picture is so useful that we will go one step further, and consider an infinitesimal change in position. Instead of $\Delta\rr$, we will write $d\rr$ for the vector between two points which are infinitesimally close together. This is illustrated in Figure 3.1, which shows a view of the curve through an “infinite magnifying glass”.
Note that, like any vector, $d\rr$ can be expanded with respect to $\ii$, $\jj$, $\kk$; the components of $d\rr$ are just the infinitesimal changes $dx$, $dy$, $dz$, in the $x$, $y$, and $z$ directions, respectively, that is \begin{equation} d\rr = dx\,\ii + dy\,\jj + dz\,\kk \label{drdef} \end{equation} You may find this intuitive notion of $d\rr$ as an infinitesimal vector displacement to be helpful in visualizing the geometry of vector calculus.
What is the infinitesimal distance $ds$ between nearby points? Just the length of $d\rr$! We have \begin{equation} ds = |d\rr| \label{dsdef} \end{equation} and squaring both sides leads to \begin{equation} ds^2 = |d\rr|^2 = d\rr\cdot d\rr = dx^2 + dy^2 + dz^2 \label{ds1} \end{equation} which is just the infinitesimal Pythagorean Theorem, as shown in Figure 3.2. 2)